Self-Replicating Turing Machines and Computer Viruses

Elise de Doncker
Artificial Life X. Workshop Proceedings on Machine Self-Replication, pp. 129-132.
2006

Download PDF (48.03Kb) (You need to be registered on forum)
[Back to index] [Comments (0)]

Elise de Doncker
Western Michigan University, Kalamazoo, MI 49008, USA
elise@cs.wmich.edu

Abstract
Self-replication
Recursive and partial recursive functions
Church-Turing Thesis
Recursive and recursively enumerable sets
Questions about self-replicating programs/TM
Application to Computer Viruses
Conclusions
Acknowledgments
References

Abstract

This paper reviews self-replication in the context of (partial) recursive functions and Turing computability. By the Church-Turing thesis, these are equivalent to other models of computation. The theory is linked to applications in the area of computer viruses. We address the views of various authors with respect to the (in)adequacy of Turing machine equivalent models for computer viruses.

Self-replication

The book “Gödel, Escher, Bach, An Eternal Golden Braid”, by Douglas Hofstadter (Hofstadter, 1999) gives examples of self-replication (self-rep) and self-reference (self-ref).

Hofstadter lists a self-replicating computer program which, called with a “template” argument as speciﬁed in the procedure declaration part, calls itself recursively with its own text as the template, resulting in delivering itself as output. It is noted that the program consists of two parts, the procedure deﬁnition and the recursive call where it uses the template data.

In the example of self-replication of DNA, parallels are drawn between self-rep in DNA and self-ref in a formal logic system, the Typographical Number System (TNT). For example, DNA strands correspond to TNT strings, genetic code to Gödel code, and translation of RNA ⇒ proteins to arithmetization from 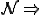$\cal{N} \Rightarrow$ to meta TNT. As a futher analogy, one strand of the double-stranded DNA piece is referred to as the template since it does not encode the DNA enzymes endonuclease, polumerase and ligase.

In the remainder of this paper we review recursive and partial recursive functions, the Church-Turing thesis, recursive and recursively enumerable sets, and self-replicating programs/Turing machines. We furthermore discuss an application to computer viruses and related computability issues.

Recursive and partial recursive functions

In this section we deﬁne partial recursive and recursive functions operating on strings of symbols. The deﬁnition can be transformed to natural numbers through Gödel numbering.

Let us use the introductory deﬁnition in (Brainerd and Landweber, 1974) of (partial) recursive functions. An alphabet 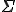$\Sigma$ is a non-empty, ﬁnite set of symbols. 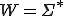$W = \Sigma^*$ is the set of all strings that can be made with symbols from 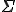$\Sigma$ and also includes the empty string, $\epsilon$ .

In view of the recursive nature of the deﬁnition following, we need a set of basis functions:

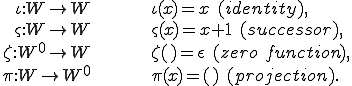
$\begin{align} \iota : W \mapsto W && \iota(x) = x\ (identity),\\ \varsigma : W \mapsto W && \varsigma(x) = x + 1\ (successor),\\ \zeta : W^0 \mapsto W && \zeta() = \epsilon\ (zero\ function),\\ \pi : W \mapsto W^0 && \pi(x) = ()\ (projection). \end{align}$

The recursion proceeds with the use of four operators on functions:

$f \circ g(x) = f(g(x))\ (composition),\\ f \times g(x,y) = (f(x),g(y))\ (combination),\\ f^y(x) = f \circ f \dots \circ f\ (exponentiation,\ y\ times\ composed),\\ f^\bigtriangledown(x,y) = x'\text{ where }f^k(x,y) = (x', 1)$

and 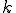is the smallest value such that the second argument listed becomes 1 (repetition). Repetition may not be deﬁ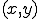ned at (x,y) in view of the fact that successive compositions of 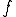may never yield 1 as the second argument.

A partial recursive function 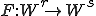$F : W^r \mapsto W^s$ is either one of the basis functions, or obtained from these by a ﬁnite number of compositions, combinations, exponentiations or repetitions. This corresponds to the ability to implement a partial recursive function as a program in an algorithmic language; the program may not terminate for all arguments as the function may not be everywhere deﬁned. A recursive function is partial recursive and total (deﬁned for all arguments). As a simple example, 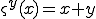$\varsigma^y(x) = x+y$ is a recursive function deﬁned in terms of successor and exponentiation.

Church-Turing Thesis

As an amazing result/claim, the classical Church-Turing thesis states that the set of the recursive functions as deﬁned above coincides with that of the functions which can be implemented by any algorithmic means (and terminate for all arguments). Computational models including those of Turing machines (TM), Post systems, and algorithmic programming languages, are all equivalent. This can be extended to partial recursive functions by allowing, e.g., programs/TM which do not halt for all inputs in the sense that termination is guaranteed for arguments where the function is deﬁned, but may not be otherwise.

By Gödel numbering, the strings in a language are mapped to natural numbers, and the string membership problem in a language is mapped to classifying natural numbers with respect to some characteristic. In this context, (Hofstadter, 1999) lists various versions of the Church-Turing thesis, of different strenghts. The “standard” version goes as follows: “Suppose there is a method which a sentient being follows in order to sort numbers into two classes. Suppose further that this method always yields an answer within a ﬁnite amount of time, and that it always gives the same answer for a given number. Then some general recursive function exists which gives exactly the same answers as the sentient being’s method does”. The “isomorphism version” (which strengthens the conclusion) is: “Suppose there is a method which a sentient being follows in order to sort numbers into two classes. Suppose further that this method always yields an answer within a ﬁnite amount of time, and that it always gives the same answer for a given number. Then some general recursive function exists which gives exactly the same answers as the sentient being’s method does. Moreover, the mental process and the recursive function are isomorphic in the sense that on some level there is a correspondence between the steps being carried out in both computer and brain”, also suggesting that the logical structure of this calculation (on a high enough level) in the brain can be implemented as a recursive function.

If we consider (partial) recursive functions giving an answer to decision problems, then recursive functions can be implemented by procedures which always halt and give a YES/NO answer in all instances of the problem addressed; whereas partial recursive functions are only guaranteed to give a YES answer for instances of the problem where the answer is, indeed, afﬁrmative.

Recursive and recursively enumerable sets

A recursive set L is recognized by a TM which decides the membership problem in L, thereby accepting inputs 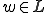$w \in L$ and rejecting otherwise. Here the membership problem is decidable, corresponding to a recursive characteristic function for L. For a recursively enumerable (r.e.) set, the membership problem is semi-decidable (which falls in the undecidable class). For an r.e. 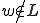language L there is a TM which accepts strings $w \in L$ but may not halt for $w \not\in L$ . In this case, L has a partial recursive characteristic function.

As an example, the universal language

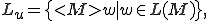
$L_u = \{< M > w | w \in L(M)\},$

where 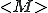< M > is a binary encoding of TM M and 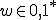$w \in {0,1}^*$ , is r.e. but not recursive. This relates to the undecidability of the halting problem (for TM); i.e., it is undecidable to determine for an arbitrary TM M and input w, whether or not M will halt with input w.

Furthermore, a language is r.e. iff there is a TM which enumerates the strings of the language on its tape.

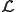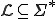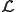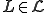A property $\cal{L}$ of r.e. languages is a set of r.e. languages $\cal{L} \subseteq \Sigma^*$ , such that L is said to have property $\cal{L}$ if $L \in \cal{L}$ (Hopcroft and Ullman, 1979). 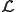$\cal{L}$ is called a trivial property if 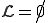$\cal{L} = \not0$ or if it consists of all r.e. languages. Instead of studying 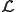$\cal{L}$ , we focus on a set of encodings 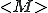< M > of TM M corresponding to its languages L(M), i.e.,

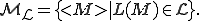
${\cal{M}}_{\cal{L}} = \{< M > | L(M) \in \cal{L} \}.$

It is well-known that every non-trivial property 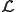$\cal{L}$ of r.e. languages is undecidable, corresponding to the non-recursiveness of 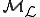$\cal{M}_{\cal{L}}$ for non-trivial $\cal{L}$ .

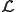Some properties are r.e. whilst other ones are not. For example,

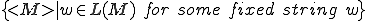
$\{< M > | w \in L(M)\ for\ some\ fixed\ string\ w\}$

is r.e., and

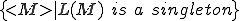
$\{< M > | L(M)\ is\ a\ singleton\}$

is not r.e.

Questions about self-replicating programs/TM

With a basis of theoretical computer science aspects in previous sections, we now turn to questions related with self-replication. These may be of practical importance, for example, to check whether a given program replicates itself accurately. Consider a program 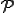$\cal{P}$ which outputs strings. Some questions are:

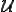Is it possible to write a program $\cal{U}$ that, when given 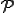$\cal{P}$ as input, determines if 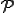$\cal{P}$ outputs (replicates) itself (as one of its outputs)?
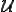Is it possible to write a program $\cal{U}$ that, when given 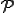$\cal{P}$ as input, determines if 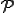$\cal{P}$ outputs only itself?
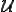Is it possible to write a program $\cal{U}$ that, when given 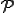$\cal{P}$ as input, determines if 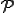$\cal{P}$ replicates itself within a set number of steps or set time?

These questions can be formulated with the expectation that 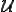$\cal{U}$ would decide the problem (give a yes/no answer for each instance of the problem); or, with the expectation that 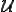$\cal{U}$ would output “yes” in the afﬁrmative case but may not otherwise give an answer.

For example, the set

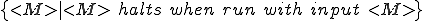
$\{< M > | < M >\ halts\ when\ run\ with\ input\ < M >\}$

is r.e. but not recursive.

Application to Computer Viruses

Programs that replicate themselves have been important in the study of computer viruses. A computer virus is deﬁned by (Cohen, 1985) as a program that can infect other programs by modifying them to include a (possibly evolved) copy of itself (so that a virus can spread to the transitive closure of information paths from an initial source).

This gives rise to the deﬁnition of a viral set, the elements of which produce other elements of the set upon execution. Cohen uses a Turing machine model where each virus in a viral set produces an element of the set on some part of the TM tape outside of the original virus speciﬁcation.

Formally, a viral set is a pair (M,V) where M is a TM and V is a set of viruses written as strings in the tape alphabet of M. When M (in its start state) reads 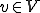$v \in V$ , it writes a string 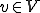$v \in V$ somewhere else on its tape.

In (Thimbleby et al., 1998), the notion of viral infection is associated with the following attributes:

A trojan (Trojan horse) component, since an infected program behaves in an unwanted manner under some conditions;
A dormancy component, as the infection may conceal itself;
An infective component, since infected programs are destined to infect other programs.

Cohen’s undecidability results (Cohen, 1985; Cohen, 1987; Cohen, 1989; Chess and White, 2000) show that

There is no algorithm that can detect all viruses. Some infected ﬁles may be missed (false negative); or non-infected ﬁles may be detected as infected (false positive); or no answer may be returned.
There is no algorithm (TM) that can decide if one virus evolves into another.

Other results (Chess and White, 2000) include that there are viruses for which no error-free detection algorithm exists (undetectable computer viruses).

For the study of trojans and computer viruses, a number of authors have pointed out inadequacies with the classic (TM equivalent) computation models. According to (Wegner, 1996; Wegner, 1997; Thimbleby et al., 1998), TM equivalent models are not sufﬁcient to describe systems that interact. A virus entering a system indeed constitutes an interaction (Thimbleby et al., 1998).

(Thimbleby et al., 1998) also show that the virus biological metaphor is inadequate. They introduce a new framework for modelling computer viruses and other malicious programs, and make suggestions for the construction of virally resistant systems.

(Mäkinen, 2001) comments on (Thimbleby et al., 1998) and uses a universal TM (UTM) at the basis of his model for computer viruses. In this model, simulation of a viral TM v by the UTM produces a viral TM v' on the tape of the UTM. (Mäkinen, 2001) ﬁnds the UTM model suitable for addressing basic undecidability problems related to computer viruses.

In their reply to Mäkinen’s paper, (Thimbleby et al., 2001) comment, e.g. that, whilst Mäkinen’s model is appropriate for basic undecidability issues, virus replication is too narrowly speciﬁed; and the formalism fails to address infection mechanisms, which makes it hard to explore virus prevention.

Conclusions

We draw analogs between self-replicating programs (”machines” in general) and self-replicating Turing machines, based on the Church-Turing thesis. Sayama (Sayama, 2006) (this conference) addresses similar problems based on links between von Neumann’s universal constructors and Turing machines.

We distinguish between recursive sets (decidable problems), sets which are r.e. but not recursive (semi-decidable problems) and non-r.e. sets. The latter two correspond to undecidable problems. The question can be raised whether being r.e. but not recursive has applications in practice.

Furthermore we discuss computer viruses and related computability issues in the framework of self-replicating programs.

Acknowledgments

The reviewers’ comments, especially regarding the application to computer viruses, are greatly appreciated.

References

Brainerd, W. S. and Landweber, L. H. (1974). Theory of Computation. John Wiley and Sons.
Chess, D. M. and White, S. R. (2000). An undetectable computer virus. In Virus Bulletin Conference. http://www.research.ibm.com/antivirus/SciPapers/VB2000DC.htm.
Cohen, F. (1985). Computer viruses. Dissertation, USC.
Cohen, F. (1987). Computer viruses: Theory and experiments. Computers and Security, 6:22–35.
Cohen, F. (1989). Computational aspects of computer viruses. Computers and Security, 8:297–298.
Hofstadter, D. R. (1999). Gödel, Escher, Bach: An Eternal Golden Braid. Basic Books, Perseus Book Group.
Hopcroft, J. E. and Ullman, J. D. (1979). Introduction to Automata Theory, Languages and Computation. Addison-Wesley.
Mäkinen, E. (2001). Comment on ’A Framework for Modelling Trojans and Computer Virus Infection. Computer Journal, 44(4):321–323.
Sayama, H. (2006). Self-replicating machines attempting to solve the unsolvable. Workshop on Machine Self-Replication, Tenth International Conference on the Simulation and Synthesis of Living Systems (ALife X).
Thimbleby, H., Anderson, S., and Cairns, P. (1998). A framework for modelling trojans and computer virus infection. Computer Journal, 41(7):444–458.
Thimbleby, H., Anderson, S., and Cairns, P. (2001). Reply to ‘Comment on ”A Framework for Modelling Trojans and Computer Virus Infection”’. Computer Journal, 44(4):321–323.
Wegner, P. (1996). The paradigm shift from algorithms to interaction. http://jeffsutherland.com/ // papers/wegacm.pdf.
Wegner, P. (1997). Why interaction is more powerful than algorithms. Commun. ACM, 40(5):80–91.

[Back to index] [Comments (0)]

VX Heavens