Eric Filiol, Edouard Franc, Alessandro Gubbioli, Benoit Moquet, Guillaume Roblot
PROCEEDINGS OF WORLD ACADEMY OF SCIENCE, ENGINEERING AND TECHNOLOGY VOLUME 23, pp.373-379
ISSN 1307-6884
August 2007
Download PDF (465.73Kb) (You need to be registered on forum)© 2007 WASET.ORG
E. Filiol is with the Lab. of Virology and Cryptology, ESAT, B.P. 18, 35998 Rennes Arm´ees (France), Email: eric.filiol@esat.terre.defense.gouv.fr. He is also Full Professor at ESIEA - Laval filiol@esiea.fr
Edouard Franc, Benoit Moquet and Guillaume Roblot are with the Lab. of Virology and Cryptology, ESAT, B.P. 18, 35998 Rennes Arm´ees (France) and with the French Navy, ESCANSIC, Saint Mandrier, France.
Alessandro Gubbioli is with the Polytecnico di Milano, Milan, Italy and was on stay at the Lab. of Virology and Cryptology, ESAT for this research work.
Worm propagation profiles have significantly changed since 2003-2004: sudden world outbreaks like Blaster or Slammer have progressively disappeared and slower but stealthier worms appeared since, most of them for botnets dissemination. Decreased worm virulence results in more difficult detection.
In this paper, we describe a stealth worm propagation model which has been extensively simulated and analysed on a huge virtual network. The main features of this model is its ability to infect any Internet-like network in a few seconds, whatever may be its size while greatly limiting the reinfection attempt overhead of already infected hosts. The main simulation results shows that the combinatorial topology of routing may have a huge impact on the worm propagation and thus some servers play a more essential and significant role than others. The real-time capability to identify them may be essential to greatly hinder worm propagation.
Keywords - Combinatorial worm, worm spreading, worm virulence, stealth worm, spreading simulation, vertex cover, network topology, WAST simulator, SuWAST simulator.
A number of recent studies [11], [12], [13] have addressed the problem of fast spreading worms on Internet-like networks. Among others, Staniford and al. [11] have presented and evaluated several highly worm virulent possible techniques such as hit-list scanning, permutation scanning, Internet-sized hit-lists... Their study was based on spreading data of former worms like Code Red I, Code Red II and Nimda. Moreover they considered worms that could spread more slowly (surreptitious worms) but in a much harder to detect contagion fashion. Their hypothesis is that such new worm technologies could theoritically subvert upwards of 10,000,000 Internet hosts. Finally they present a few robust mechanisms that would enable an attacker to control and update already deployed worms.
Other studies [12], [13] have later on confirmed Staniford and al.'s analysis. However all these studies and models are generally derived from known worms spread and most of the potential scenarii for superworms - Currious yellow worm, Warhol worm, Flash worm -,are up to now of theoretical intererest only. Based on probabilistic extrapolation, none of them have been of course tested on a real network or even in a simulation environment close enough to real networks - up to the authors' knowledge.
This paper presents a new worm two-step propagation strategy on a totally unknown network. The related worm has been called Combinatorial worm. In the first step, the worm first "learns" the network configuration both at micro (local) and macro levels. From that knowledge, the worm then set up a two-level malicious network by means of Dynamic Host Tables (DHT) and graphs. In a second step, some particular optimal structures of the built graph - cover vertex set - are identified by the attacker and used to efficiently and surreptitiously manage, update and control the malicious network. The main features of the strategy presented here is two-fold: first the worm does not need any a priori knowledge about the network, second the level of connection overhead (wrong, useless worm connections) is optimally lowered. Our spreading model describes very well how web-based malware [10], among other possible examples, could optimally propagate.
The essential interest of our study lies on the fact that this propagation strategy has been experimentally tested on two dedicated, powerful simulation environment, specially designed in our laboratory for our study: WAST (Worm Analysis and Simulation Tool) [4] and SuWAST (Super Worm Analysis and Simulation Tool) [5]. The paper is organised as follows. Section II presents our working propagation scenario. Section III focuses on the malicious network optimal management by means of the vertex cover set. Section IV then presents the two simulation environments we have designed and the implemtation issues with respect to our propagation scenario. Section V gives detailed results of our simulation while Section VI concludes and addresses some future work.
The aim is to design a worm initial infection strategy of an unknown network with the following constraints:
The worm in fact organizes the whole target network into a two-level hierarchy. Each time a machine is newly infected, one or two DHT (Kademlia-like [7], [8]) structures are set up and updated by the worm with the data related to its spreading activity according to the following scheme:
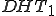structure is set up and use a malicious P2P network. This network will be called worm lower network or worm P2P network. It is dedicated to the local maganement of dynamic address hosts;
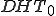structure is set up and used to manage the worm at a macro level. This higher level of the network will be denoted worm upper network. This means that static hosts will manage two DHT structures 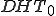and ;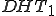
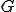. This structure will manage fixed IP addresses (typically those of servers) only. It is maintained at the attacker's side.These two structures are connected at the fixed IP addresses'level. Moreover, the attacker has a monitoring machine which collects data sent by every infected machine. The overall, upper level topology of the malicious network is then managed at the attacker's level through the graph structure 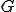. The two-level organisation of the malicious network is summarized in Figure 1.
Fig. 1. Network partition according to the two-level propagation strategy. The worm lower networks are contained into the different ellipses (green links maneged by local 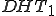structures) while the worm upper network is composed of static addresses (generally servers; red links managed by local 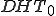structures)
The choice of a two-level structure aims at making the worm spread as invisible as possible. From one given node, the worm spreads only to nodes that used to communicate with it: existing previous connection (leaving some IP traces whithin local machines) between them can be considered as a "trust" relation.
Once the initial spread to the network has occured, a second step, denoted worm management occurs (see Section III).
This step aims at finding IP addresses to infect.
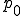, the worm generates a random IP adress from the local IP address. The four IPv4 fields of the address are modified. Then the worm tries to infect this random (remote) IP address.The value of parameter 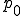is freely customized but it should not excess 0.1 as confirmed by our simulation results presented in Section V. The worm must be able to determine whether a given target is already infected or not. This point will be developped further in Section IV.
Each time a worm copy succeeds in infecting a new machine, it first initializes a (local) 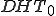structure and then checks whether the local address is a static or a dynamic one.
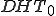. This structure contains only one static address (see next item). 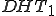structure dedicated to manage only static addresses at the upper level. This new static IP address is also included in the new local 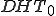structure. Consequently, the different local 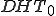structures are all connected by a single point to the 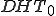structures. It is worth mentioning that the choice of the static address "connecting" 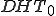and 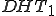structures, is free. As an example, it may be the last static IP address that has been infected by the worm and every time a new static address is found and infected, a new 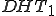structure is locally used.In order to monitor the worm activity and to evaluate its efficiency, the attacker needs to define and use some indicators. In order to define the topography of the worm upper network, we need to know which addresses have been infected, from which machine and at what time. Thus the corresponding graph structure 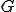which describes the worm upper network is defined as follows:
is connected to node 
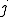if machine 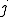has been infected by machine .By definition (particularly when considering the fact that a machine cannot infect an already infected machine), the resulting graph structure is a simple directed graph. In order to settle thing down, let us suppose that machine successfully managed to infect machine 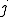at time 
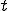. Then every new copy of the worm (e.g. on machine j) sends the following data structure back to the attacker's monitoring machine:
At the worm lower network level, any newly infected machine (e.g. with a dynamic address) will then send the following data to the single fixed IP address present in the 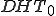structure:
These data are sent to the attacker's monitoring machine according to the following rules:
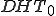structure send data only to the single machine in this structure which has a static address;The purpose of these first data is to help to build the model and to measure how quickly the whole (simulated) network is infected (worm propagation speed and efficiency). In other words, if we start with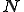 
machines, how many time does it take to infected the whole network?
A second indicator is used in order to evaluate the ratio of useless connections during the spread. In other words, we want primarily determine the number of attempts of infecting already infected machine. Thus at every infection attempt, a given machine sends back the following data:
Every data sent by any copy of the worm will be protected against eavesdropping. Thus the data may be either encrypted or protected by steganography (or vovert channel). This part has been only partly implemented during our final experimentation.
Once the initial step has been performed (the worm has infected any possible machine), the attacker must be able to control, set up or modify the worm behavior. For that purpose, he must be able to connect to the network, to "talk" with one (or more) worm copy. Then the worm copy will spread the new setup to the other worm copies.
To connect to the worm network, the attacker may either use a dedicated tool looking for some infected machine or exploit the data sent back to his monitoring machine during the initial infection step.
Locally at the local machine level, the DHT structures (both 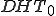and 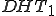) must be managed in order to avoid a too much increase of their size. Consequently, a time aspect has been introduced. Systematically, the single fixed IP address is included in the DHTs of a given machine while this structure dynamically manages and keeps only the IP addresses corresponding to machines that recently established a connection and that are susceptible to infection with respect to the worm. As in Kademlia [8], we use a node identification system based on node ID built from the local IP address essentially and the XOR metrics.
Additionally, we used a weighted measure for every IP address in the DHTs tables. Without loss of generality, let us consider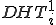 
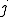of machine . For every other IP address in 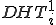, let us denote 
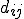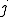the (XOR) distance between machines and and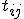 
the last connection time (in seconds) between machine and 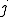. Thus, we attribute the following weight to each of them:
.
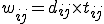So, 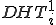permanently self-updates in order to keep only the IP addresses with lowest weight 
.
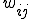Once a sufficient amount of data has been collected, the main approach is to use them in order to efficiently manage the upper network. Indeed, we just have to limit ourselves to the fixed addresses of the whole malicious network since each of them will then locally cooperate/communicate with the other worm instances at the lower network level.
The main objective is to limit the overhead during the management and thus reduce the number of connections and data sent. We will use the fact that there exists a natural "connection hierarchy" between servers. As an example, Server A generally connects to Server B which then connect itself to Server C. This implies that generally Server A does not connect to Server C. Once again, the aim is to make the worm spread according to the "natural" or "ad hoc" connections between servers. If Server A does generally not connect to Server C, an alert may be raised in case of such a connection is initiated by a worm. This context being considered, our aim is to model the connections between fixed addresses by means of a directed graph 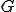which is progressively built/updated by the attacker on its monitoring machine:
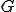, denoted 
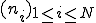are representing fixed IP addresses (generally a server); 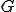are defined by:
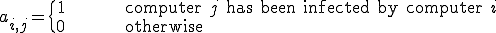
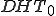It is essential to consider a directed graph since connection may be one-way. Moreover, we may consider a weighted directed graph as well by introducing a time aspect as previously. Let us recall that aside the overall graph , the different structure are locally managed in the same way as 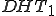structures are. The difference lies in the nature of the IP addresses (static or dynamic).
When the attacker wants to automatically (or not) manage every worm copy (e.g. to update or upgrade the worm with new exploits dedicated to newly found software flaw), the aim is to limit as much as possible the communication overhead. The aim is thus to identify a few "privileged" nodes that enable to optimally or at least efficiently communicate with all other nodes.
These conditions being fixed, one possible solution is to consider the vertex cover problem for a graph. Let us recall its definition.
Definition 1: Let 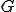a undirected graph 
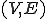. The vertex cover is a subset 
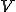of the vertices of the graph which contains at least one of the two endpoints of each edge:
.
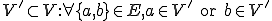On the graph of Figure 2, the subset {2, 4, 5} is a vertex cover of 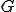. Moreover, it is the smallest possible one. Thus, from the
Fig. 2. Exemple of Graph with Vertex Cover of Size 3
data collected during the initial spreading phase, the attacker will first try to identify a vertex cover (let us recall however that it is a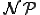 
-complete problem). Then, if the attacker wants to manage the upper network, he will proceed as follows:
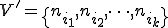. Of course, he may consider a partial subgraph to minimize the complexity of the search algorithm.
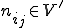with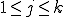 
, only. 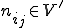will then spread locally to other nodes of the graph according to a suitable ordering limiting the probability for a node to be updated by two nodes nij in the vertex cover (for exemple, in Figure 2, node 3 can be updated either by node 2 or node 4, but only node 2 will).The use of a vertex cover set - hence our naming of Combinatorial worm - thus minimizes the number of communications between nodes while covering all the nodes quite simultaneously. Whenever a static node of the cover set receives a new information/command, the spread switches at the lower network level.
The attacker has to find the smallest possible vertex cover set for this graph. Since this problem is an NP-complete optimisation problem, this is the most critical issue and most of the time we are bound to search for near optimal vertex cover set only. Different approximation algorithms have been used in our experiments:
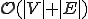;Two simulation environment have been designed to test, evaluate and validate worm propagation scenarii on large-scale networks.
The first one is WAST (Worm Analysis and Simulation Tool) [4]. He has been developped in our laboratory by Alessandro Gubbioli, from the Politecnico di Milano, Italy. He was designed to simulate limited-scale networks (up to a few tens of hosts) and thus validate in a exploratory, preliminary step, some particular propagation strategies.
The purpose was to develop a system that allows simulations of network's attack, in a controlled environment, at application level, instead of packet level. This approach is profitable mainly because:
The simulation's result could be useful to validate the correctness of these models and to compare the effectiveness of different attack strategies. Moreover, WAST can be used to stress protection tools in order to verify their reaction capabilities in front of unknown threat. It offers two macro-functionalities:
The first one has been realized through a honeypot's network, described later. The second functionality consists of a set of scripts that offer specific services and extend the honeypot's capabilities.
The core of WAST is build around honeyd, an open source project to create an instrument for managing virtual low-interaction honeypot [9]. Honeyd is a framework for virtual honeypots that simulates computer systems at the network level. Honeyd supports the IP protocol suites and responds to network requests for its virtual honeypots according to the services that are configured for each virtual honeypot. The simulated computer systems appear to run on unallocated network addresses.
Due to lack of space, we will neither present WAST in detail nor describe its use for a particular worm strategy. The reader may refer to [4] for a complete description of both issues.
The SuWAST (Super Worm Analysis and Simulation Tool) environment has been built from scratch using the two standalone tools FakeNetbiosDGM et FakeNetbiosNS written in C language by Patrick Chambet [1]. These programs are based on the Netbios transfer protocol, developped by IBM and Sytec in the early 80's.
FakeNetbiosDGM is a program which allows periodic emission on the port 138 of several broadcasts which all seems to come from a number of Windows hosts. It mimicks the network Netbios datagram service. This service enables to send a message either to a group name (multicast or broadcast) or to a unique name (unicast) in a non-connected. As for FakeNetbiosNS, it operates on the port 137. When listening this port it answers to name resolution requests, among others things. It mimicks the "Netbios Name Service" which associates a host name to an IP address.
The ability to generate and to send UDP packets on a given port (FakeNetbiosDGM) and the ability to listen a given port and to forge an answer (FakeNetbiosNS) make these two utilities very insteresting to build SuWAST.
Thus, we have a powerful simulation environment of complex, heterogenous networks (clients, servers, routers...), allowing simulations of network attacks, in a controlled environment at packet level. If SuWAST is more complex to set up and manage than WAST, on the contrary it enables large-scale simulations. As an example, we have been able to simulate up to a 60,000-host heterogeneous network on a single 2 GB machine (Pentium 4 3Ghz). It is also possible to interconnect such machines to simulate heterogeneous networks of millions of hosts.
SuWAST simulates a network as follows:
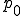are set up;The network initialisation step is performed by a single script, which is automatically generated.
The complete SuWAST technical documentation is available in [5].
In order to ease the implementation of our strategy, each simulated node (clients and servers) embeds a data structure containing various (random) fields:
From a practical point of view, the worm may use a given infection marker (e.g. a mutex denoted A) for any dynamic address (P2P level) and use a different one to identify infected machine with fixed address (e.g. a mutex denoted B).
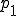, close to 1;Whenever the worm infects a node, it just reads these informations instead of really collecting them and eventually updates them (in particular the INF_MARK field). Then the code is far easier to develop for our simulation purposes.
To launch the propagation a first host is randomly selected and infected. It then spreads according to our scheme. We call a propagation instance a triplet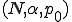 
where 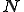is the number of simulated hosts in the network and the 
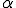neighborhood parameter.
Numerous scenarii have been extensively simulated and analysed on either WAST or SuWAST. Due to lack of space, we will present one of the most interesting one, only. All the other ones are described in [6]. The topology of the network is the following:
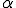other servers and different client hosts (randomly ranging from 16 to 32). The server neighborhood parameter with respect to other servers has been proved to be far more essential that the other possible neighborhood parameters. We have tested ![\alpha\in[1,5]](../img/cache/d6ba549365dccc55fd903c6d386aa158.gif)
;
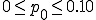.The simulated network contains 100 servers and a grand total of 3000 hosts in average. Simulations have been conducted 20 times. The results are summarized in Figure 3.
Two metrics have been used:
,
.
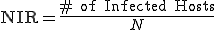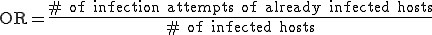As a first general result, the whole network is infected quite instantly. Of course all hosts are simulated on the same machine and thus it is not obvious at all that the simulated propagation time would be of the same order of the propagation time on a real, Internet-like network. However, in the simulation hosts are sequentially executing while in a real network hosts are working in parallel. Further developments on our simulator will take parallel computing and network load into account. But, mathematical extrapolations clearly show that our propagation scenario would indeed require a few seconds to infect a Internet-like network with a quite excellent network infection rate.
Three essential results are noticeable (see also Figure 3):
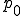has a significant impact on both the Network Infection Rate (NIR) and the Overinfection Rate (OR). The case 
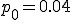is optimal, provided that the server neighborhood parameter 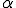is not to large (see hereafter);
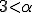(server neighborhood parameter), most of the results being closer to 99 %. Whenever 
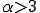, the probability to have hosts or subnetworks without any connection with infected hosts, decreases very fast;![\alpha\in[3,6]](../img/cache/c462dac51e32bb654f44748b3e0108d9.gif)
.As far as the infection overheard (OR) is concerned, the analysis has clearly shown that is has a local impact only. In other words, useless infection attempts (the host is already infected) originated only from close hosts in terms of the DHT metrics used. A traffic analysis is likely to see these connections as normal since all these hosts use to communicate.
In conclusion, the best parameter values for this propagation strategy are 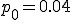and .
In this paper, we have designed, tested and analysed the behaviour of a so-called combinatorial worm. Two main features make this worm very efficient:
As a consequence, the main conclusion is that a number of servers - those which are in the vertex cover set - are more important than the other ones. From the defender's side, the issue of identifying those particular (server) hosts may help to more efficiently and more quickly prevent such worms to operate and finally eradicate them from the network. On a more general level, for any kind of worm, modeling the malicious network as graph and searching for particular graph structures (e.g. vertex cover set) could help to increase defense against worms and botnets propagation.
Future work will consider new indicators to test the reactiveness of our worm once the network has been infected. The purpose will be to evaluate how the worm copies can communicate the one with the another, what is the effect on server crashes on the worm activity... Networks disturbances have also to be simulated to test the worm's robustness. Parallel computing should also enable to improve simulation realism.
![Fig. 3. Network Infection Rate (NIR) and Overinfection Rate (IR) for \alpha\in[0, 5] and 0 \le p_0 \le 0.10](img/aef05/fig3.jpg)
Fig. 3. Network Infection Rate (NIR) and Overinfection Rate (IR) for ![\alpha\in[0, 5]](../img/cache/fb2dc8bac5ba8da097952c740b9199f3.gif)
and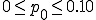
Future work will also consider the development of a worm intelligence and study worm program cooperation within a network. We may consider two or more different worms, one acting at the upper network level and cooperating with the second one at the lower network level. One step farther couls be to consider a different worm code for every different lower networks (polymorphic/metamorphic generation of a child worm - lower network level - by the parent worm at the upper level). Then, this would make suitable settings in order to determine what are the most optimal ways of cooperation between a parent worm and its children.