N. Goranin, A. Cenys
Journal of Engineering Science and Technology Review 2 (1) (2009) pp.43-47
ISSN 1791-2377
May 2009
Download PDF (131.5Kb) (You need to be registered on forum)Received 30 March 2009; Accepted 18 May 2009
© 2009 Kavala Institute of Technology. All rights reserved.
Internet worms remain one of the major threats to the Internet infrastructure. Modeling allows forecasting the malware propagation consequences and evolution trends, planning countermeasures and many other tasks that cannot be investigated without harm to production systems in the wild. Existing malware propagation models mainly concentrate on malware epidemic consequences modeling, i.e. forecasting the number of infected computers, simulating malware behavior or economic propagation aspects and are based only on current malware propagation strategies. Significant research has been done in the world during the last years to fight the Internet worms. In this article we propose the extension to our genetic algorithm based model, which aims at Internet worm propagation strategies modeling under pressure of countermeasures. Genetic algorithm is selected as a modeling tool taking into consideration the efficiency of this method while solving optimization and modeling problems with large solution space. The main application of the proposed model is a countermeasures planning in advance and computer network design optimization
Keywords: Internet worm, genetic algorithm, model, evolution, countermeasures.
The number of malware in the wild is constantly increasing [1]. Despite the significant shift in motivation for malicious activity that has taken place over the past several years: from vandalism and recognition in the hacker community, to attacks and intrusions for financial gain which has been marked by a growing sophistication in the tools and methods used to conduct attacks, thereby escalating the network security arms race [2] and leading to domination of botnets in the current malware landscape [3] internet worms remain among the most significant threats to the Internet infrastructure. According to [4] they cover approximately 14% of the current malware landscape and [1] notices that the most widely reported new malicious code family in 2008 was the Invadesys worm, and 4 other worms took their places in Top10 of new malicious code families. The recent outbreak of the Conficker worm [5] shows that the worm problem remains relevant and requires further analysis.
Worms are network viruses, primarily replicating on networks. Usually a worm will execute itself automatically on a remote machine without any extra help from a user. However, there are worms, such as mailer or mass-mailer worms, that will not always automatically execute themselves without the help of a user [6]. In this article we analyze and model Internet worm propagation strategies, since their replication mechanisms differ significantly from mailer and mass-mailer worms [7]. Propagation strategy is one of the most descriptive malware characteristics [8]. Propagation of most worms is rapid (compared with classical computer viruses) and aggressive. Worms such as CodeRed and Nimda have been persistent for longer than 8 months since their introduction date. As worms spread through nearly all networks, they find nearly all of the weakest hosts accessible and begin their lifecycle anew on these systems. This then gives worms a broad base of installation from which to act [9]. The main issues faced in worm evaluation include the scale and propagation of the infections [9]. Modeling allows Internet worm researchers to predict damage for a new worm threat [10], understand the behavior of malware, including spreading characteristics [11], understand the factors affecting the malware spread, determine the required effectiveness of countermeasures in order to control the spread and facilitate network designs that are resilient to malware attacks [12], predict the failures of the global network infrastructure [13]. Since significant research has been done in the world during the last years to fight the Internet worms the worm evolution has a tendency to changes. Our proposed model [7] extension allows modeling the Internet worms' propagation strategies evolution under the pressure of countermeasures. Genetic algorithm [14] was selected as a modeling tool since it simulates natural selection by means of repeatedly evolving population of solutions (malware propagation strategies in our case) and therefore may be used for predicting and modeling possible future propagation strategies. Genetic algorithm modeling has been proved to be effective in many areas such as business decision making, bioinformatics and other [15-18].
We define the Internet worms propagation strategy as a combination of methods and techniques, used by the worm to achieve tasks assigned to it by the worm creator. So the strategy suitable to achieve one specific task (e.g., creating the botnet) may be not useful for another (e.g., disrupting Internet functioning). Modern worms are usually created on a modular basis and may contain all or some of the following parts [9]: a reconnaissance module, that scans the Internet for vulnerable hosts; an attack module, that may exploit from one to many known vulnerabilities at potentially vulnerable host; a communication module that allows worms to communicate between themselves or to transfer information to the worm management center; a command module, that allows to accept commands; and an intelligence module, that insures functioning of the communication module, since it contains information how to find a neighbor worm for communication. Specific methods used in each of the modules are called patterns and a strategy can be also defined as a combination of patterns. A strategy is also dependent on worm introduction techniques, i.e. method used to release worm to the wild, connection protocol used (e.g. Transmission Control Protocol (TCP) or User Datagram Protocol (UDP)), etc. Since the number of existing and historic worms is high, we will describe only two propagation strategies used by CodeRed and Ramen, since they represent two different attitudes in complexity, vulnerable platform and functionality and can provide an understanding of strategies used in the wild.
On June 18th 2001 a serious Windows IIS vulnerability was discovered. On July 13th 2001 Code Red worm version 1 that exploited this single vulnerability was released. Due to a code error in its random number generator, it did not propagate well. 10:00 UTC of July 19th Code Red version 2 was released with the corrected random generator. It generated 100 threads. Each of the first 99 threads randomly chose one IP address and tried to set up connection on port 80 with the target machine (if the system was an English Windows 2000 system, the 100th worm thread would deface the infected system's web site, otherwise the thread was used to infect other systems, too) [10]. The worm was programmed to scan hosts in /8 with a 50% probability, /16 - with 37.5% probability and with 12.5% probability it would scan a totally random network [9]. Sub-networks 127.0.0.0/8, loopback, 224.0.0.0/8, multicast were excluded [13]. If the connection was successful, the worm would send a copy of itself to the victim web server to compromise it and continue to find another web server. If the victim was not a web server or the connection could not be setup, the worm thread would randomly gene-rate another IP address to probe. The timeout of the Code Red connection request was programmed to be 21 seconds. Netcraft web server survey showed that there were about 6 million Windows IIS web servers at the end of June 2001 [10]. More than 350.000 of them were infected in several hours [19].
The Ramen worm appeared in January 2001. Ramen attacked RedHat Linux 6.0, 6.1, 6.2, and 7.0 installations, taking advantage of the default installation and three known vulnerabilities: FTPd string format exploits against wu-ftpd 2.6.0, RPC.statd Linux unformatted strings exploits, and LPR string format attacks. This vulnerable software could be installed on any Linux system, meaning the Ramen worm can affect other Linux systems, as well. The worm acted in the following way: defaced any Web sites it found; disabled anonymous FTP access to the system; disabled and removed the vulnerable rpc.statd and lpd daemons, and ensured the worm would be unable to attack the host again; installed a Web server on TCP port 27374, used to pass the worm payload to the child infections; removed any host access restrictions and ensured that the worm software would start at boot time; notified the owner (worm creator) of two e-mail accounts of the presence of the worm infection. Worm then began scanning for new victim hosts by generating random class B (/16) address blocks (scans were restricted from 128/8 to 224/8, the most heavily used section of the Internet). Web server acted as a small command interface with a very limited set of possible actions. The mailboxes served as the intelligence database, containing information about the nodes on the network. This allowed the owners of the database to be able to contact infected systems and operate them as needed [9].
The first epidemiological model of computer virus propagation was proposed by [20]. Epidemiological models abstract from the individuals, and consider them units of a population. Each unit can only belong to a limited number of states. A SIR model assumes the Susceptible-Infected-Recovered state chain and SIS model - the Susceptible-Infected-Susceptible chain. Sheila et al. in [21] use the epidemiological model as a basis for botnet modeling. The model is modified from the general model based upon the type of infection, transfer modality, and potential for re-infection and can be represented as a M-S-E-I-R chain, where M is the class of computers (hardware or software) who are not infected with malware that can be exploited to enable bot infestation; S is used to represent the class of computers that are infected during manufacture with malware that can be exploited to enable bot infestation. E is the set of computers that have been infected, are not transmitting the infection, and in whom the infection has not been detected; I is the set of computers that have been infected, are transmitting the infection, and in whom the infection has not been detected; R is the set of computers that have been infected, whose infection has been detected, and that have had their bot removed.
In a technical report [22] Zou et al. described a model of e-mail worm propagation. The authors model the Internet e-mail service as an undirected graph of relationship between people. In order to build a simulation of this graph, they assume that each node degree is distributed on a power-law probability function.
Lelarge in [23] introduces an economic approach to malware epidemic modeling (including botnets). He states that users and computers on the network face epidemic risks. Epidemic risks (propagating viruses and worms in this case) are risks that depend on the behavior of other entities (externalities) in the network. The model based on graph theory quantifies the impact of such externalities on the investment in security features in a network. Each agent (user) can decide whether or not to invest some amount to self-protect and deploy security solutions that decrease the probability of contagion. When an agent self-protects, it benefits not only to those who are protected but also to the whole network. If all agents invest in self-protection, then the general security level of the network is very high since the probability of loss is zero. But a self-interested agent would not continue to pay for self-protection since it incurs a cost c for preventing only direct losses that have very low probabilities. When the general security level of the network is high, there is no incentive for investing in self-protection. This results in an under-protected network.
Li et al. [24] model botnet-related cyber-crimes as a result of profit-maximizing decision-making from the perspectives of both botnet masters and renters/attackers. From this economic model, they derive the effective rental size and the optimal botnet size. Fultz in [25] describes distributed attacks organized with the help of botnets as economic security games.
The Random Constant Spread (RCS) model [19] was developed by Staniford et al. using empirical data derived from the outbreak of the CodeRed worm. It assumes that the worm has a good random number generator that is properly seeded. The model assumes that a machine cannot be compromised multiple times and operates several variables: K is the constant average compromise rate, which is dependant on worm processor speed, network bandwidth and location of the infected host; a(t) is the proportion of vulnerable machines which have been compromised at the instant t, Na(t) is the number of infected hosts, each of which scans other vulnerable machines at a rate K per unit of time. But since a portion a(t) of the vulnerable machines is already infected, only K(1-a(t)) new infections will be generated by each infected host, per unit of time. The number n of machines that will be compromised in the interval of time dt (in which a is assumed to be constant) is thus given by:
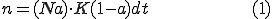
N is assumed to be a large constant address space so the chance that worm would hit the already infected host is negligible. From this hypothesis:
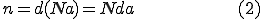
It is also possible to write
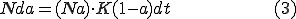
From this
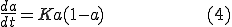
where
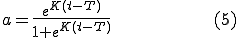
So the model can predict the number of infected hosts at time t if K is known. The higher is K, the quicker the satiation phase will be achieved by worm. As [9] states, that although more complicated models can be derived, most network worms will follow this trend.
Other authors [26] propose the discrete time model (AAWP), in the hope to better capture the discrete time behavior of a worm. However, according to [13] continuous model is appropriate for large-scale models, and the epidemiological literature is clear in this direction. The assumptions on which the AAWP model is based are not completely correct, but it is enough to note that the benefits of using a discrete time model seem to be very limited.
On the other hand Zanero et al in [13] propose a sophisticated compartment based model, which treats Internet as the interconnection of autonomous systems, i.e. sub-networks. Interconnections are a so-called "bottlenecks". The model assumes, that inside a single autonomous system (or inside a densely connected region of an AS) the worm propagates unhindered, following the RCS model. The authors motivate the necessity of their model via the fact that the network limited worm Saphire which was using UDP protocol for propagation was following the RCS model till the "bottlenecks" were flooded by its scans.
Zou et al in [27] propose a two-factor propagation model, which is more precise in modeling the satiation phase taking into attention the human countermeasures and the decreased scan and infection rate due to the large amount of scan-traffic. The same authors have also published an article on modeling worm propagation under dynamic quarantine defense [28] and evaluated the effectiveness of several existing and perspective worm propagation strategies [29].
Malware propagation in Gnutella type Peer-to-Peer (P2P) networks was described in [12] by Ramachandran et al. The study revealed that the existing bound on the spectral radius governing the possibility of an epidemic outbreak needs to be revised in the context of a P2P network. An analytical model that emulates the mechanics of a decentralized Gnutella type of peer network was formulated and the study of malware spread on such networks was performed.
Ruitenbeek in [30] simulates virus propagation using parameterized stochastic models of a network of mobile phones, created with the help of Mobius tool and provides insight into the relative effectiveness of each response mechanism. Two models of the propagation of mobile phone viruses were designed to study the impact of viruses on the dependability and security of mobile phones: the first model quantifies the propagation of multimedia messaging system (MMS) viruses and the second - of Bluetooth viruses.
In their presentation Zou et al. [31] suggest using botnet propagation model via vulnerability exploitation and notice some similarities of bot and worm propagation. We can not aggree with this statement since botnets use more propagation vectors than worms do. Botnet propagation modeling using time zones was proposed by Dagon et al. [32]. The model uses diurnal shaping functions to capture regional variations in online vulnerable populations.
Authors of [33] have developed a stochastic model of P2P botnet formation to provide insight on possible defense tactics and examine how different factors impact the growth of the botnet.
In [7] we proposed the genetic algorithm based model, which was dedicated to evaluating existing as well as modeling other potentially dangerous Internet worms' propagation strategies at initial propagation phase. The efficiency of strategies was evaluated by applying the proposed fitness function. The proposed model was tested on existing worms' propagation strategies with known infection probabilities. The tests have proved the effectiveness of the model in evaluating propagation rates and have shown the tendencies of worm evolution. We have also proposed the genetic algorithm (GA) based propagation rate estimation model [8] which evaluated the negative (decrease) change of population size after satiation phase of a newly appearing worms by generating a decision tree based on a statistical data of known worms.
Since the full model description would require too much space and is available in [7] here we provide only the general model description. The model consists of a propagation strategy representation structure (each strategy is represented as a chromosome), GA acting under specified conditions and a fitness function, which evaluates the strategy's infection rate at the initial propagation phase, leaning on probability and time consumption estimations of strategy's used methods. We have chosen to model strategies for a theoretical Internet worm, which aims infecting the largest amount of hosts during a fixed relatively short period of time. Model is based on the adopted GA: during the initialization stage initial population of strategies is generated. At selection stage strategies are selected through a fitness-based process and in case termination condition is not met evolutionary mechanisms are started. In case termination condition is reached, algorithm execution is ended.
Initial population is generated on a random basis, i.e. each individual, representing separate worm propagation strategy is combined of random genes' values. Population size N is equal to 50. Population size remains constant after each new generation. The combined termination condition was selected. The algorithm would stop producing new generations in two cases: either the number of generations has reached 100, or the fitness evaluation of the fittest individual in a population remains constant for 10 consecutive generations. The crossover point for each pair of parents is selected randomly and defines the gene, after which the crossover operation is performed. The mutation operator defines the gene of a newly generated individual that should change value from current to any other random value from the range of possible gene values. Mutation operator is activated to each newly generated individual with a 0.005 probability. Fitness proportionate selection was used. The sample generated strategy may look like:
Si=(IP_GEN="Random, excluding 127.0.0.0/8, loopback, 224.0.0.0/8, multicast"; OS_PLATF="Apple OS"; TRANSF="Connection oriented"; EXPL_1=" CVE-2007-3876"*; EN_EXPL_2="False"; EN_EXPL_3="False"; EN_EXPL_4="False"; EN_EXPL_5="True"; EN_EXPL_6="False"; EN_EXPL_7="False"; EN_EXPL_8="False"; EXPL_2="-"; EXPL_3="-"; EXPL_4="-"; EXPL_5=" CVE-2004-0485"**; EXPL_6="-"; EXPL_7="-"; EXPL_8="-"; EN_MEM="False"; MEM="-"; EN_HIER="True"; HIER="Autonomous"; EN_COM="False"; COM="-"; EN_EXEC="True"; EXEC="Update functionality"; EN_ADD="True"; ADD="Write to MBR to remain after reboot"; EN_EVOL="False"; EVOL="-").
The proposed model provides a general framework for evaluating different worms' propagation strategy parameters. The proposed model was tested on existing worms' propagation strategies with known infection probabilities and was used for forecasting Internet worm propagation strategy evolution in case no countermeasures are taken.
In order to evaluate countermeasures efficiency on worm propagation it is necessary to classify them. In this article we use the countermeasures taxonomy proposed by Brumley et al. in [34]. The fitness function used in our previous model [7] which does not evaluated the efficiency of countermeasures was written as
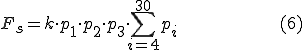
where: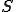 
- evaluated strategy; 
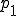- probability that the generated IP address exists and alive, 
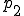- probability that host is running the OS platform that the worm supports, 
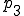- probability that worm will be successfully transferred to the potential victim, 
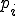- probability that the ith gene will result in an infected host, i=4..30; 
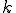- the number of cycles the worm, using the evaluated strategy, can perform in one second time interval.
The taxonomy [34] contains several countermeasure types: Reactive Antibody Defense (signatures, patching after worm break-out); Reactive Address Blacklisting (blocking the the connections from known infected hosts); Proactive Protection (universal system hardening based on worm disorientation); Local Containment ("good neighbor" blocking the outgoing worm scans if infected). We do not evaluate the technical problems related with the deployment of each countermeasure type, but it is obvious that their deployment is time dependant, since it takes time to prepare signatures, disseminate and constantly update blacklist, etc. It is also unarguable that worm spread becomes time dependant and the rate will decrease not when satiation phase is reached but much earlier. In that case Eq.6 can be rewritten as
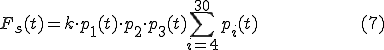
Variable 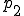is not time-dependant since we assume that the number of computers running the OS is constant (negligible percent of users will change OS for example from Windows to Linux or vice versa in case a new worm appears) and the disorientation measures will effect in exploit efficiency. Each 
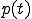can be described as a curve
which shows the decrease of probability. In real life all countermeasures would be used in combination. Due to that fact the function p(t) representing the probability decrease in time would be an approximation of the real statistical data. Currently no such data is available and systematic data collection is needed in order to create such curves. Eq.7 could be used to draw the curve of a specific worm propagation strategy that would be decreasing in time. In order to compare efficiency of different strategies under pressure of countermeasures we propose the new fitness function:
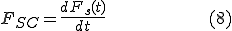
which is equal to time derivative of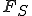 
. Derivative shows the strategy's efficiency decrease rate. The lower is decrease the more efficient the strategy is.
All other model assumptions and limitations do not change. We could not check the efficiency of the proposed model extension due to the lack of statistical data but the framework proposed allows modeling of Internet worm evolution under pressure of countermeasures. It is also important to note that different countermeasure proportions may lead to different probability curves and worm strategy evolution. The future work should be concentrated on the collection of statistical data and its modeling.
In this article we have proposed the extension to our genetic algorithm based model, which aims at Internet worm propagation strategies modeling under pressure of countermeasures. Extension is based on assumption that probability of infection is time-dependant and is decreasing over time when countermeasures are being deployed. The proposed fitness function selects the evolving strategies by evaluating the decrease rate of their efficiency. Due to the lack of statistical data we can not forecast what combination of countermeasures would be the most effective in each case and future work should be concentrated on the collection of statistical data and its modeling.
The proposed model can be used as a framework in computer network design optimization. Genetic algorithm is selected as a modeling tool taking into consideration the efficiency of this method while solving optimization and modeling problems with large solution space.