Jeffrey Kephart, William Arnold
In Proceedings of the 4th Virus Bulletin International Conference, R. Ford, ed., Virus Bulletin Ltd., Abingdon, England, 1994, pp. 178-184
1994
Download PDF (622.29Kb) (You need to be registered on forum)One way that anti-virus programs identify the presence of a virus in an executable file, a boot record, or memory is by using short identifiers called signatures, which consist of sequences of bytes in the machine code of the virus. A good signature is one that is found in every object infected by the virus, but is unlikely to be found if the virus is not present; i.e. the likelihood of both false negatives and false positives must be minimized. Typically, a human expert chooses a signature for a new virus by means of a laborious, time-consuming procedure. Unfortunately, the accelerating influx of new computer viruses threatens to outpace the ability of human experts to analyze and find signatures for them.
To help alleviate this burden, we have developed a statistical method for automatically extracting good signatures from the machine code of a virus. The basic idea is to characterize statistically a large corpus of programs (currently about half a gigabyte), and then to use this information to estimate false-positive probabilities for proposed virus signatures. In effect, the algorithm extrapolates from the corpus to the much larger universe of executable programs which do or might exist. In practice, signatures extracted by this method are very unlikely to generate false positives, even when the scanner that employs them permits some mismatches.
This patent-pending technique has been used to either extract or evaluate the more than 2500 virus signatures used by IBM AntiVirus. It obviates the need for a small army of virus analysts, permitting IBM's signature database to be maintained by a single virus expert working halftime.
One of the most widely-used methods for the detection of computer viruses is the virus scanner, which uses short strings of bytes to identify particular viruses in executable files, boot records, or memory. The byte strings (referred to as signatures) for a particular virus must be chosen such that they always discover the virus if it is present, but seldom give a false alarm. Typically, a human expert makes this choice by converting the binary code of the virus to assembler, analyzing the assembler code, picking sections of code that appear to be unusual, and identifying the corresponding bytes in the machine code.
Unfortunately, new viruses and new variations on previously-known viruses are appearing at a high rate, as illustrated by Fig. 1. For the last several years, IBM's High Integrity Computing Laboratory has been collecting new viral strains from anti-virus researchers around the world. In June, 1991, the rate at which new viruses were added to the collection was approximately 0.6 per day. By June, 1994, the rate had quadrupled to approximately 2.4 per day. Other researchers, using a somewhat different (but equally valid) method for counting the number of distinct viruses, report that the current rate at which new viruses are written is about 5 per day. In any case, it cannot be denied that the high rate of new viruses is creating a heavy burden for human experts, who must spend an increasing proportion of their valuable time performing a task that demands both a high level of skill and a high tolerance for tedium.
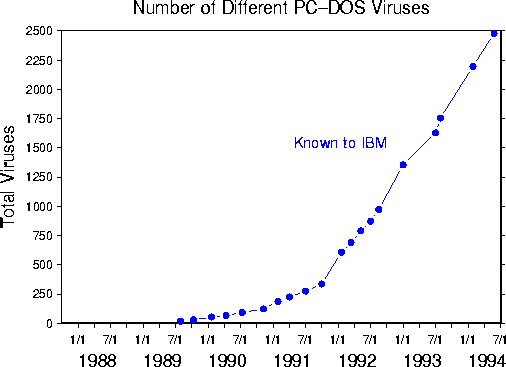
Figure 1: Cumulative number of viruses for which signatures have been obtained by IBM's High Integrity Computing Laboratory vs. time.
In order to alleviate this problem, we have developed a statistical method for automatically extracting near-optimal signatures from computer virus code. The algorithm examines each sequence of code in the virus and estimates the probability for that code to be found in legitimate software. The code sequence with the lowest ``false-positive'' probability is chosen as the signature. IBM has used this technique to extract nearly 2000 virus signatures. In addition, it has been used to evaluate and improve hundreds of signatures which had been chosen previously by human experts.
The existence of an automatic technique for signature extraction also opens the possibility of ameliorating a long-criticized deficiency of virus scanners: the delay between when a virus first appears in the world and when a signature capable of recognizing that virus is distributed to an appreciable fraction of the population. At the High Integrity Computing Laboratory, we are planning to eliminate this delay for a large class of viruses by incorporating automatic signature extraction into an automatic immune system for computer networks [1].
First, in section 2, we shall explain briefly some of the philosophy and pragmatics underlying the use of virus scanners and signatures. Then, in section 3, we shall describe the signature extraction/evaluation algorithm in some detail. As will be seen, the probability estimates generated by the algorithm must be calibrated before the algorithm can be used to extract or evaluate signatures; a method for doing this is described in section 4. Section 5 presents some results which demonstrate that the algorithm does an excellent job of discriminating between good and bad signatures. In section 6, I describe briefly an automatic immune system that we are planning to implement, of which the signature extractor is a vital component. We conclude in section 7 with a brief summary.
For simplicity, let us first consider file-infecting viruses that infect their host programs with exact or near-exact copies of themselves. Self-garbling viruses, particularly those which are polymorphic, have naturally received most of the hype and hoopla, but a majority of PC DOS viruses -- even those found to in actual incidents -- are of this ``simple'' type.
Suppose that we wish to determine whether a particular host program P is infected with a particular simple virus V. The most obvious method would be to scan the machine code of P, looking for a pattern of bytes that exactly matched V. However, there are several practical problems with this approach. Typical computer viruses are a few hundred to a few thousand bytes in length. Given that there are several thousand PC DOS viruses (and thus several thousand patterns to be matched), the amount of memory required just to contain all of the patterns would be several megabytes, which would be prohibitive. Second, it would be dangerous for anti-virus software to contain a large library of known viruses. Virus writers would no doubt be very grateful if we were to make virus collections so easily accessible to them.
Rather than requiring an exact match, the typical practice is to use just a small piece of the virus code as a means for identification. These short templates, called signatures, are much easier to handle, and reveal nothing useful to virus authors. There is an additional, very important advantage to using short signatures: they still work even when other parts of the virus change.
There are two sources of viral mutation. First, viruses are sometimes modified deliberately by humans who wish to produce new viral strains without having to take the trouble to write one from scratch. However, the new strain will still be detected unless the change is made somewhere in the sequence of bytes corresponding to the virus signature.1
The second source of viral mutation is programmatic. A small but growing minority of viruses are programmed to modify their form deliberately whenever they replicate in an attempt to evade detection by virus scanners. Generally, this is done by garbling the main portion of the virus using a key that is selected randomly at the time of replication. When the transmuted virus is loaded into memory and executed, the first several bytes of code (the ``head'') degarbles the main portion of the virus, which is then executed. However, the ``head'' is often a fixed sequence of bytes, and a signature can be selected it. A small portion of today's viruses are able to overcome this deficiency by randomly generating a large number of different heads, which may or may not possess the same functionality. These polymorphic viruses present more of a challenge to anti-virus technology. So far, human experts have been able to devise detection algorithms for all such viruses; the algorithms tend to employ methods that are much more complex than simple signature scanning.
Although short signatures allow one to capture much possible variation, there is a significant drawback to their use. The shorter the signature, the more likely it is to be found in some perfectly legitimate code just by coincidence. To minimize this possibility, experts choose sequences of bytes which look unusual to them. This tedious technique works adequately for the most part. However, it is not uncommon for a new release of a virus scanner to be followed quickly by numerous reports of false positives generated by one of the new signatures. Some in the anti-virus industry feel that false positives are a worse problem than viruses themselves because they create panic, confusion, and unnecessary work, and undermine people's faith in anti-virus technology. No matter what the signature, one can not guarantee that false positives will never occur, but it is imperative that the false-positive probability be reduced to acceptable levels.
Human-selected signatures for viruses that have been written in high-level languages are particularly prone to false positives because most of the generated code is taken verbatim from libraries specific to the compiler. Unless the expert spends an unconscionable amount of time familiarizing himself with the boring details of the machine code typically generated by every C, FORTRAN, Pascal, etc. compiler in the world, he will not be qualified to judge whether a particular sequence of bytes is really unusual. This is a job for a computer, not a human being!
In order to increase the likelihood of capturing new variations of a previously-known virus, some virus scanners (for example the one employed by IBM AntiVirus) recognize inexact matches between scanned bytes and signatures as a mutant strain of a known virus. The benefits of capturing a broader range of mutations must be weighed against the increased probability of a false positive. Again, human experts are not in a good position to make such a tradeoff because it is nearly impossible for them to quantify how much more risk is involved.
To summarize, a signature must satisfy two conflicting criteria. The signature (and its associated matching criterion) must capture a broad variety of conceivable mutations for a particular virus, but the false-positive probability must be as low as possible. Ultimately, the tradeoff must be based on human judgment, but that judgment must be founded on a reasonable estimate of the false-positive probability. The next two sections of this paper describe an algorithm for obtaining such an estimate.
Suppose that we have just obtained a sample of a new virus imbedded in some host (infected) executable program. We wish to find a good signature for that virus: one that will appear in every instance of the virus, but is extremely unlikely to appear just by coincidence in code not containing the virus.
This is accomplished in two phases. First, a set of signatures that are likely to appear in each instance of the virus is generated. Second, one or a few signatures that minimize the false-positive probability are chosen from this set.
In our virus isolation laboratory, we use the following procedure to identify portions of the virus that are likely to be invariant from one instance to another. An automatic algorithm runs the infected sample on a DOS machine, and then tries to lure the virus into infecting a diverse suite of ``decoy'' programs. A decoy's sole purpose in life is to become infected. To increase the chances of success in this noble, selfless endeavor, decoys are designed to be as attractive as possible to those types of viruses that spread most successfully. A good strategy for a virus to follow is to infect programs that are touched by the operating system in some way. Such programs are most likely to be executed by the user, and thus serve as the most successful vehicle for further spread. Therefore, the algorithm entices a putative virus to infect the decoy programs by executing, reading, writing to, copying, or otherwise manipulating each of them. Such activity tends to attract the attention of many viruses that remain active in memory even after they have returned control to their host. To catch viruses that do not remain active in memory, the decoys are placed in places where the most commonly used programs in the system are typically located, such as the root directory, the current directory, and other directories in the path. The next time the infected file is run, it is very likely to select one of the decoys as its victim. From time to time, each of the decoy programs is examined to see if it has been modified. Any that have been modified are assumed to have been infected with the virus, and are stored in a special directory, where they await the next processing step.
After having obtained several infected decoys, the infected regions of the decoys are compared with one another to establish which regions of the virus are constant from one instance to another. Usually, most of the virus is constant, with one or more small regions that vary. In some cases, there is a fairly short constant region near the beginning of the virus, followed by a large variable region; this is indicative of a simple self-garbling virus. In a small percentage of cases, the constant regions are so short as to be useless for the purpose of extracting signatures. Such a situation indicates that the virus is at least moderately polymorphic, and in this case the algorithm gives up, and a human expert performs the analysis. Further improvements to the algorithm could be made to handle certain types of polymorphism, but there will always be a place for human virus experts!
Provided that the virus is not overly polymorphic, there are at this point one or more sections of the virus which tentatively have been classified as being invariant. However, it is quite conceivable that not all of the potential variation has been captured within the samples. Various heuristics are employed to identify portions of the ``invariant'' sections of the virus which by their nature are unlikely to vary from one instance of the virus to another. In particular, ``code'' portions of the virus which represent machine instructions (with the possible exception of bytes representing addresses) are typically invariant. ``Data'' portions of the virus, which for example could represent numerical constants, character strings, screen images, work areas for computations, addresses, etc. are often invariant as well, but are much more vulnerable to modification by the virus itself when it replicates itself or by humans who intentionally modify viruses so as to help them elude virus scanners. We use a variety of techniques to segregate code and data portions, and only the code portions are retained for further processing.
At this point, there are one or more sequences of invariant machine code bytes from which viral signatures could be selected. We take the set of candidate signatures to be all possible contiguous blocks of S bytes found in these byte sequences, where S is a signature length specified by the user or determined by the algorithm itself. (Typically, S ranges between approximately 12 and 36.) The remaining goal is to select from among the candidates one or perhaps a few signatures that are least likely to lead to false positives.
Before describing the selection process, it is worth noting two things. First, the aforementioned procedure for generating the candidate signatures is not crucial. Any other technique, including manual labor by a human expert, could be used. Second, the number of candidate signatures could be very small -- even just one. This would be appropriate if one were using the signature extractor to evaluate a signature that has been chosen previously, most likely by a human expert.
The key idea behind the algorithm is to estimate the probability that each of the candidate signatures will match a randomly-chosen block of bytes in the machine code of a randomly-chosen program, either exactly or with some specified number or pattern of mismatches. In the case of extraction, we select one or more signatures with the lowest estimated ``false-positive'' probabilities of all the candidates, making sure that this probability is less than some established threshold. In the case of evaluation, we just place a seal of approval on a signature if its estimated false-positive probability is less than the established threshold. Thus the problem of signature extraction or evaluation is reduced to the following problem: For a given sequence of S bytes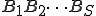 
(call it 
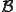for short), estimate the probability 
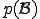for 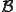to occur in a large body of normal, uninfected code.
The most obvious way to compute 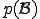is to tally the number of occurrences of 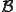in a large corpus of uninfected programs. Call this quantity 
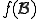. Then 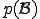could be estimated as simply
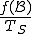(1)where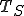 
is the number of S-byte sequences in the corpus.
However, there is a serious problem with this technique. Suppose that the corpus is reasonably large -- on the order of a gigabyte or so. For relatively common sequences (ones that could be expected to appear several times per gigabyte), the probability estimate given by Eq. 1 would be reasonably accurate. Somewhat common sequences (ones that could be expected to appear once or twice per gigabyte, or once in every few gigabytes) might or might not appear in the corpus. Extremely rare sequences almost certainly would not appear in the corpus. It is readily apparent from these considerations that the technique prescribed in Eq. 1 has very little ability to discriminate between somewhat common and very uncommon sequences. Another way to express this is that the dynamic range of possible probability estimates yielded by this method is inadequate; it cannot produce estimated probabilities less than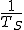 
, or about 
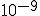for a gigabyte corpus.
A more illustrative way to understand the inadequacy of this technique is by making an analogy to a problem encountered in training machines to understand human speech. In order to make sense of a stream of phonemes that have been extracted from an utterance, it is often useful to have a language model that is derived from a large corpus of utterances. The problem is similar to that of estimating the probability that a given sentence will be uttered, given a large corpus of previous utterances. For example, suppose that we have access to a recording of all press interviews with United States senators during the 1980's, and that we would like to estimate the probability for each of the following three sentences to be spoken by a U.S. Senator sometime during the 1990's:
The 1980's corpus would probably consist of tens or hundreds of millions of sentences. Within that corpus, we might expect sentence 1 to appear several times. It would be somewhat surprising to find an instance of sentence 2 in the corpus, but not absolutely inconceivable. Sentence 3 seems extremely unlikely. It is not the sort of sentence that one would expect to occur naturally in ordinary human discourse; it has the look of something generated by a somewhat incompetent computer program.
The most likely scenario is that one would find several instances of sentence 1 in the 1980's corpus, but no instances of sentences 2 and 3. Under these circumstances, the method of Eq. 1 would assign an estimated probability of zero to sentences 2 and 3. It would fail to distinguish sentence 2 as being unusual, but significantly more likely than sentence 3.
In fact, less than halfway through the 1990's, we find that sentence 1 has indeed been uttered several times. But we also find that sentence 2 has been uttered at least once -- by Senator Phil Gramm of Texas, who made his stunning confession on June 7, 1994, after the question of his extraterrestial origin was posed by a reporter from The Weekly World News [2]. As far as we are aware, the world is still waiting for sentence 3.
There is a critical need for an algorithm capable of distinguishing the likelihood of sentence 2 as much greater than that of sentence 3, even if neither one appears in the corpus. Fortunately, researchers in the field of speech recognition have been dealing with just this sort of problem for many years. The solution is to collect statistics on short sequences of adjacent words. Trigrams (sequences of three adjacent phonemes or words) are fairly popular in the speech community. The key insight is that reasonably good statistics can be obtained for sufficiently short sequences. Then, a simple approximation formula can be used estimate the probability of a long sequence by combining the measured frequencies of the shorter sequences from which it is composed.
In sentence 2, the sequences ``It's all true'' and ``we are'' are quite common, and ``space aliens'' is only somewhat unusual, so the overall sentence can be classified as unusual, but not terrifically so. In sentence 3, none of the individual words are very unusual, but the sequences ``American space god'', and ``space god aliens'' are quite unusual, and contribute to a very low overall estimated probability for the sentence. In effect, the trigram technique (which is easily generalized to higher-order n-grams) allows one to extrapolate beyond an existing corpus to a vastly larger universe of statistically similar utterances. This permits one to discriminate between somewhat unusual and extremely unusual utterances.
The technique that we have developed for automatic signature extraction is completely analogous to this standard speech recognition technique. Suppose that trigram statistics were tallied for a large corpus. Then the estimated probability for the sequence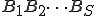 
would be calculated from
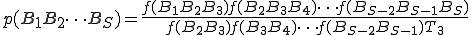(2)where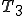 
is the number of trigrams in the corpus.
To get some insight into the derivation of Eq. 2, consider the simpler problem of estimating the probability of a 4-byte sequence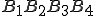 
from measured frequencies of its constituents. First, one can re-write 
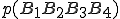in the form:
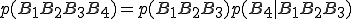(3)where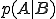 
is to be interpreted as the probability of byte sequence A having been preceded by byte sequence B. Eq. 3 is exact up to this point. However, if we suppose the correlation between byte 
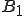and byte 
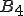is sufficiently weak that it can be ignored, the term 
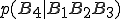can be replaced as follows:
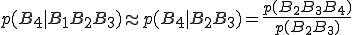(4)Inserting Eq. 4 into Eq. 3 yields
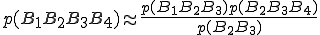(5)a special case of Eq. 2.
The extension of Eq. 2 to higher-order n-grams is conceptually trivial. The technique used to extract and evaluate IBM AntiVirus's signatures is a more sophisticated variant of Eq. 2 that incorporates measured frequencies of 1-, 2-, 3-, 4-, and 5-grams. A few additional tricks are used to solve the problem of adequate storage for the 3-, 4-, and 5-gram frequencies.2
The more sophisticated variant of Eq. 2 has some additional useful capabilities. Signatures with fixed wildcards are handled by letting the wildcards serve as demarcations between non-wildcarded regions. The estimated probabilities of all non-wildcarded regions are multiplied to obtain the overall estimated probability of the signature. To calculate estimated probabilities of signatures for which m mismatches are permitted, one can (conceptually) generate all of the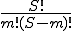 
possible mismatch configurations, treat each configuration individually as a signature with m fixed wildcards, and then add the probabilities of all configurations together. If implemented naıvely, and if m is more than 4 or 5, the combinatorics can make the computation painfully slow, even on a fast workstation. Fortunately, I have developed a recursive algorithm that bypasses the combinatorics, and obviates the need to generate each mismatch configuration explicitly. The recursive algorithm permits the estimated probability of a signature to be computed very quickly, regardless of the number of allowed mismatches.
Note that, in the speech recognition example, the trigram technique achieved good discrimination between the likelihood of sentences 2 and 3 without having any real knowledge of grammar and semantics. Similarly, the automatic signature extraction technique makes no attempt to understand code in the same way that a human expert in machine code/assembly language would. It does not know what instructions mean; in fact, it does not even know that instructions exist. It sees machine code as nothing more than a long sequence of bytes, and it applies a blind, brute-force force statistical technique to those bytes. Remarkably, this lack of understanding is more than offset by the algorithm's ability to acquire a knowledge of machine code statistics to a depth to which no human expert could or would hope to aspire. This allows the algorithm to perform extremely well, as will now be seen.
We have used two different methods to assess the quality of the signatures obtained by the extraction algorithm described in the previous section. One technique is to generate random sequences, and compare estimated and actual measured probabilities of those random sequences with one another. The resulting plot of estimated vs. actual probabilities provides a very clear picture of the algorithm's effectiveness. The second technique is to compare the estimated probabilities of signatures extracted from viruses by either the algorithm itself or a human expert, and observe the number of false positives as a function of the estimated probability. The remainder of the section treats both techniques in some detail.
Although using random sequences to characterize the relationship between estimated and actual probabilities sounds like a fine idea in principle, there is a hitch: a randomly generated byte sequence of any length is extremely unlikely to be found in any corpus. For example, there are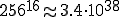 
different sequences of length 16; the probability of any given one of them being found in a 1 gigabyte corpus would be about 
.
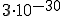The obvious solution is to reserve a section of the corpus, and choose from it ``random'' sequences that have a much better chance of having something in common with the sequences found in the rest of the corpus. In these experiments, the corpus (containing thousands of DOS, Windows, and OS/2 executable programs, comprising roughly half a gigabyte) is divided into three partitions: a small ``probe'' set, and training and test sets of roughly equal size. On the order of 10,000 sequences of s (where s is typically in the range of 12-24) contiguous bytes are drawn randomly from the probe set, and treated as candidate signatures. The probability estimation algorithm is run against the candidate signatures and the training corpus, while the number of instances of each candidate signature in the test corpus is tallied and divided by the size of the test corpus to obtain an ``actual'' probability for each signature. Then, the actual and estimated probability for each of the candidate signatures are plotted against one another on a logarthmic scale.
A typical result is displayed in Fig. 2. In this case, the candidate signature length was s=24, and no mismatches were permitted. Ideally, one would like all of the pairs of estimated and actual probabilities to fall on the dashed line, which represents perfect agreement between the two probabilities. Obviously, the algorithm falls far short of this ideal. The actual probabilities are almost always greater than the estimated probabilities because the correlations among bytes that are separated by several bytes -- which are assumed to be negligible in the approximation in Eq. 4) -- are in fact strongly positive.
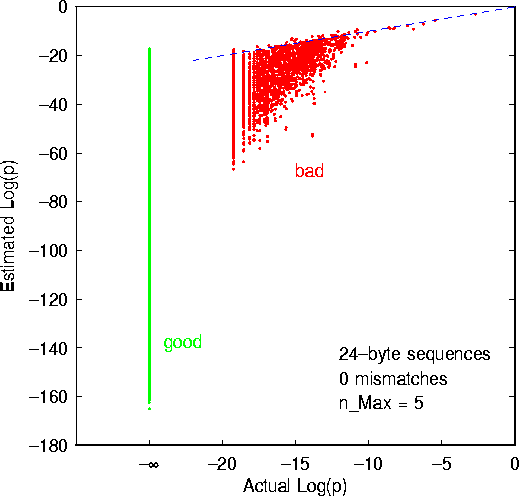
Figure 2: Estimated vs. actual exact-match probabilities for 10,535 24-byte sequences selected randomly from the probe set. Dashed line indicates equality between estimated and actual probabilities. For the several thousand probe sequences which never appeared in the test corpus, the logarithm of the actual probability is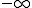 
. The estimated log-probabilities for these ``good'' sequences varied from approximately -165 to -18, resulting in a nearly-continuous vertical line at the left-hand side of the figure. The vertical striations to the right of it correspond to sequences which appeared once, twice, etc. in the test corpus. The estimated log-probabilities for these ``bad'' sequences also varied over a considerable range.
At first glance, Fig. 2 seems to contain nothing but bad news. However, the ultimate goal is not accurate probability estimation; it is simply to discriminate good signatures from bad ones. In fact, the results of Figure 2 show that this is quite feasible! Consider the vertical stripe at the left-hand side of Fig. 2. It corresponds to sequences which never appeared in the test corpus. Thus, we shall refer to them as ``good'' sequences. The cloud of points to the right of it corresponds to sequences which appeared one or more times in the reduced corpus. These we refer to as the ``bad'' sequences. In using the automatic extraction/evaluation algorithm, we must select a threshold for the estimated log-probability such that it excludes all or practically all bad sequences without eliminating too many good sequences. In this case, setting the estimated log-probability threshold at approximately -70 excludes practically all of the bad sequences, while apparently there are still many good sequences which would not be excluded. However, in order to tell exactly what proportion of good sequences are not excluded, we must look at the data in a different way.
In order to select a reasonable log-probability threshold T, we first need to compute two quantities as a function of T: the number of good sequences which are accepted by the threshold T,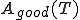 
, and the number of bad sequences which are accepted by T, 
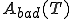. Note that 
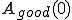and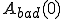 
represent the total number of good and bad sequences, respectively. Then, in order not to reject too many good sequences, we want to minimize the false-rejection probability 
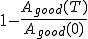, which can be done by making T as large (close to 0) as possible.
On the other hand, we also want to minimize the false-positive probability
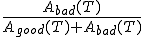, which requires that T be made as low as possible. Figure 2 displays the false-rejection and false-positive probabilities derived from the data presented in Fig. 2.
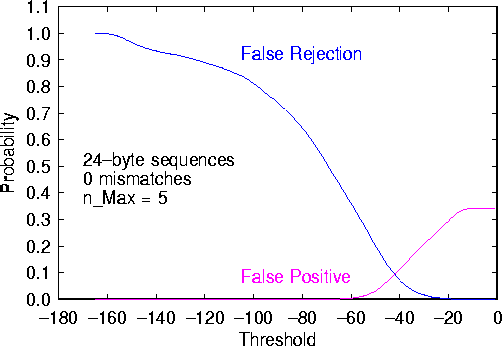
Figure 3: False-rejection and false-positive probabilities as a function of log-probability threshold T, derived from the data presented in Fig. 2.
Now we are in a position to make a well-informed tradeoff between false rejection and false positives. In this example, the false-positive probability is zero for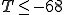 
, at which point the false-rejection probability is 48%. We can lower the false-rejection probability further by choosing 
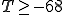, but only if we are willing to accept the chance of false positives. This can be seen clearly from Fig. 2. However, if we are willing to tolerate a false-positive probability of 0.5%, we can reduce the false-rejection probability to 36% by increasing T to -60.
What is a reasonable tradeoff? We think it is important to keep the probability of a false positive occurring in a collection of software distinct from (but similar in size to) our half-gigabyte corpus to at most a few tenths of one percent. To help illustrate what this means, suppose that we have a large collection of software containing no duplicates. In order for there to be a reasonable chance of obtaining a false positive, the size of the collection would have to be at least several hundred gigabytes. This may be on the order of the total amount of software in common usage in today's world.
The flip side of the tradeoff is the false-rejection probability. If we are extracting signatures from virus code, we can often live with a reasonably high false-rejection probability; certainly more than 50%, and perhaps even 80% or 90%. Viruses typically contain at least several hundreds or thousands of byte sequences from which to choose. We only need one or perhaps a few signatures, so we can afford to throw away many good ones. However, there are situations in which we don't have the luxury of several dozen signatures from which to choose. For example, for self-garbling viruses we must choose the signature from the head, which can be fairly short. In this case, we might be forced to raise the threshold and accept a higher false-positive probability. In the case of signature evaluation, the signature is presumably one that has been recommended by an expert. It ought to be judged on the same basis as the extracted signatures. If the signature is rejected by the threshold, the proper course of action is to obtain a sample of the virus and extract the signature automatically.
In the case of Fig. 3, one need not struggle much to find a reasonable compromise. A choice of T somewhere in the range between -60 and -70 would satisfy both of our criteria quite well.
It is interesting to note that, in Fig. 3, the false-positive probability is quite high when T=0 -- approximately 34%. In other words, out of a corpus of approximately half a gigabyte, if one chooses at random a 24-byte sequence, there is a 34% chance of finding that same 24-byte sequence somewhere else in the corpus. The moral of this is that sheer length offers little protection from the risk that a signature will generate false positives. Cleverness, be it human or algorithmic, is an essential ingredient in choosing good computer virus signatures.
We emphasize that the term ``false-positive'' probability has been used above to mean the probability of a byte sequence being found in a body of programs both statistically similar to and comparable in size to our corpus. To allow for the fact that the number of programs that exist or could exist in the world exceeds the number of programs in the corpus by a considerable margin, it might be prudent to diminish the threshold probability by a factor of 10 or 100. In other words, perhaps the log-probability threshold T should be reduced by 4 or 5. However, this may be overly conservative because a majority of virus code is written in assembler, not the high-level languages in which most of today's PC software applications are being written. Thus selection of thresholds based upon studies of probes taken from the corpus itself is likely to be overly pessimistic for viruses, which are somewhat atypical software. Practical experience indicates that, very roughly, the two effects cancel one another.
The algorithm has been used to extract most of the computer virus signatures used by IBM AntiVirus. Only a small handful of false positives have been reported. In most cases, the offending signatures have been those taken from a virus written in a high-level language such as C or Pascal. Such viruses tend to be even more of a problem for human experts than for the algorithm!
It is often difficult to extract decent signatures for such viruses because compilers tend to introduce a lot of boiler-plate code that gets intermingled with the meat of the virus code, obscuring any idiosyncracies that might be used to identify the virus. In other words, program individuality is largely washed out by compilers, making it intrinsically difficult to find a good signature. Usually, there are just a few pockets of unusual code, which can be very difficult for even the most expert of humans to find. It is hard to imagine that a human would want to be good at doing this, because it takes a lot of very specific knowledge about machine code that is produced by each of the several dozen most commonly used compilers. But the algorithm is perfectly happy to become intimately acquainted with such statistical details, and for this reason it tends to be much better than humans at extracting signatures from compiled viruses. It is easy to tell when the algorithm is working on such a virus, because almost all of the candidate signatures have very high estimated probabilities. In almost every case, the algorithm locates the pockets that contain good signature material, and chooses a signature from one of them.
We are well on the way to understanding the nature of what went wrong in the very few cases where the algorithm has selected signatures that have later proved to yield false positives. We are very optimistic about one particular idea that we think will lead to substantial improvements in the algorithm's performance on compiled viruses (stay tuned!)
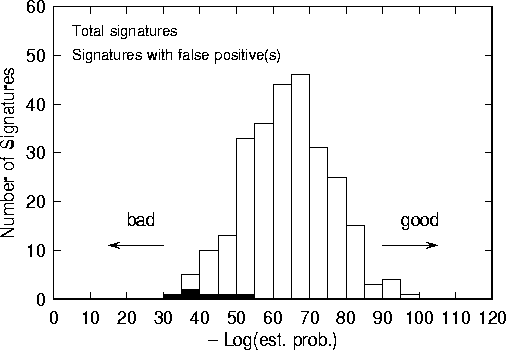
Figure 4: Histogram of estimated signature probabilities for Virus Bulletin signatures from 1991. Black histogram represents virus signatures responsible for one or more false positives.
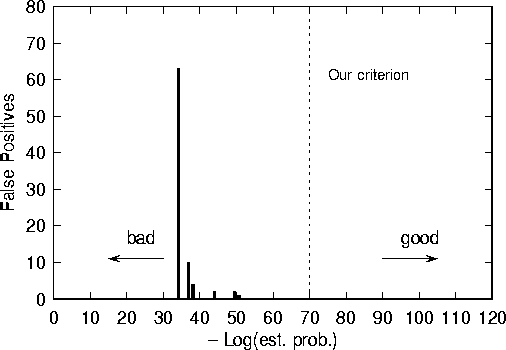
Figure 5: Number of times that each of the six ``bad'' signatures of Fig. 4 was found in the corpus, using fuzzy matching criteria. Note that all of the bad signatures have log probabilities that are much higher than our chosen threshold. In other words, the automatic algorithm would not have come close to selecting any of these poor signatures.
Another way to evaluate the performance of the algorithm is to find an alternative source of virus signatures and then check to see how the false-positive rate correlates with the probability estimated by the algorithm. The Virus Bulletin is a very convenient source of signatures. As an experiment, we took a large set of signatures that had been published in Virus Bulletin over the course of several months during mid-1991, and used the algorithm to estimate their false positive probabilities. Then, we incorporated the Virus Bulletin signatures (which were typically 16 bytes in length) into IBM's virus scanner.
The Virus Bulletin signatures were only intended to be used with exact matching. However, in order to encourage them to produce false positives, we turned on fuzzy matching, which declared a match if 12 or more of the 16 bytes matched, and scanned the corpus to see which signatures (if any) caused ``false positives''.
Out of 267 signatures, 6 yielded one or more false positives. As demonstrated in Fig. 4, the signatures that caused false positives were those for which the estimated probability was much greater than average. The signature with the highest estimated probability, Kamikaze, turned out to be the most notorious false-positive generator; it was found over 60 times in the corpus (see Fig. 5). In many cases, there were just 2 mismatched bytes. Jocker, which the algorithm claimed was one of the 5 worst signatures, turned out to be the second worst offender in the scanner test; it hit on about 10 files in the corpus.
In short, the automatic algorithmic did an excellent job of identifying signatures that were more at risk for generating false positives.
The existence of an automatic method for extracting signatures from viruses raises the possibility that a computer encountering a previously-unknown virus could develop something like an antibody to that virus without any human intervention. Removing humans from the loop could cut the response time to a new virus from several days or even several weeks to a few hours or less. The main difficulty with today's method of updating scanners is not that humans are too slow in choosing signatures; it is that the distribution mechanism for signature updates is often slow and uncertain.
Along with several of our colleagues at the High Integrity Computing Laboratory at the Thomas J. Watson Research Center, we have been designing an automatic immune system for computers and computer networks [1], for which there is a patent pending. The automatic signature extraction technique is just one of several components that have been implemented in our laboratory, and which are already supplying information that is useful for updating signature files and other databases used by IBM AntiVirus. Over the course of the next few years, our intent is that IBM AntiVirus will evolve into an immune system for computers as various components are phased into the product.
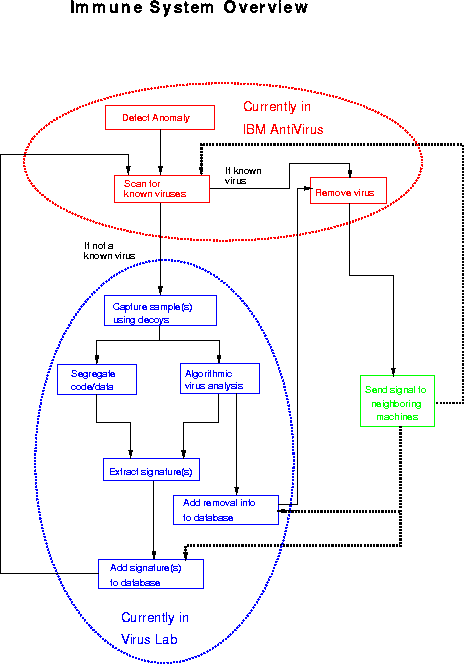
Figure 6: The main components of the proposed immune system for computers and their relationship to one another.
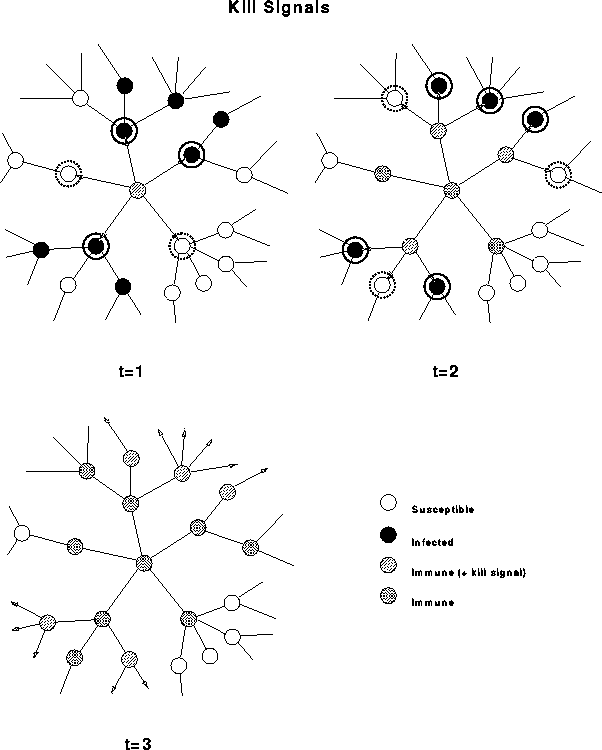
Figure 7: Fighting self-replication with self-replication. When a computer detects a virus, it eliminates the infection, immunizes itself against future infection, and sends a ``kill signal'' to its neighbors. Receipt of the kill signal results in the immunization of uninfected neighbors; infected neighbors are both immunized and prompted to send kill signals to their neighbors. Thus detection of a virus by a single computer can trigger a wave of kill signals that propagates along the path taken by the virus, destroying the virus in its wake.
The immune system (illustrated in Fig. 6) would monitor a system's memory, file system, and boot record for suspicious, virus-like behavior. Periodic scans for known viruses would take place. Any infections attributable to known viruses would be eliminated by repairing or restoring the infected host programs. To a greater or lesser degree, several of today's existing anti-virus programs include these features, and some of them integrate these functions in useful ways. The new element would be an ability to adapt to a new virus not included among the set of known viruses.
If a virus-like anomaly were detected by the immune system, the first response would be to trigger a scan for known viruses. If the anomaly could not be attributed to a known virus, the immune system would try to lure any virus that might be present in the system to infect a diverse suite of ``decoy'' programs, as described earlier in this paper. From time to time, each of the decoy programs is examined to see if it has been modified. If one or more have been modified, it is almost certain that an unknown virus is loose in the system, and each of the modified decoys contains a sample of that virus.
The next step would be to extract a signature for the virus automatically. In addition, another automatic virus analysis tool under development in our laboratory would determine how the virus attached to host programs, and extract information that would allow any program infected by the virus to be repaired.
Having automatically developed both a recognizer and a repair algorithm appropriate to the virus, the information can be added to the corresponding databases. If the virus is ever encountered again, the immune system will recognize it immediately as a known virus. A computer with an immune system could be thought of as ``ill'' during its first encounter with a virus, since a considerable amount of time and energy (or CPU cycles) would be expended to analyze the virus. However, on subsequent encounters, detection and elimination of the virus would occur much more quickly: the computer could be thought of as ``immune'' to the virus.
An additional feature, which we refer to as the ``kill signal'', would be used by a computer to inform neighboring computers on the network that it was infected. The signal would also convey to the recipient any signature or repair information that might be of use in detecting and eradicating the virus. If the recipient finds that it is infected, it would send the signal to its neighbors, and so on. If the recipient is not infected, it does not pass along the signal, but at least it has received the database updates -- effectively immunizing it against that virus (see Fig. 7).
Theoretical modeling has shown the kill signal to be extremely effective, particularly in topologies that are highly localized or sparsely connected [3, 4].
No virus detector can handle every conceivable virus, as Fred Cohen first showed by a simple adaptation of the halting problem contradiction [5]. Similarly, biological immune systems do not offer perfect protection against all diseases. The proposed computer immune system is not immune to these incontrovertible facts of mathematics and of nature. The intent is that the computer immune system should automatically deal with the myriad ``common colds'' of the virus world, and that it should alert humans when it is having trouble with a particularly nasty, difficult-to-analyze virus. Humans should only have to analyze a relatively small residue of new, especially difficult viruses.
The automatic signature extraction and evaluation algorithm has been used to extract about 2000 of IBM AntiVirus's virus signatures. Currently, the decoys are run on a specially instrumented PC, while the probability estimation is performed on an RS/6000 workstation. In a recent run, the algorithm extracted 634 signatures in just 30 minutes (not including the time required to create the virus samples).
Not only is the speed much faster than can be attained by any human expert, but the quality of the signatures (judging by IBM AntiVirus's extremely low false-positive rate) is overall at least as good as those produced by humans, and in the case of viruses written in high-level languages it may even be better.
The automatic signature extraction algorithm has greatly reduced the burden on the virus experts in our research group. We don't need to employ a dozen or more virus analyzers; instead, the virus signature database is maintained by one virus expert working halftime. This allows our virus experts to devote their skills to more challenging tasks.
Improvements are continually being made to the algorithm; the next major one will be to address the occasional false positives that are generated by signatures taken from compiled viruses. Much more exciting is the incorporation of the algorithm into a computer immune system. Over the course of the next few years, we hope to phase elements of the immune system design into IBM AntiVirus.
We are grateful to Steve White and Dave Chess for several useful lunchtime and hallway conversations, from which the idea of an automatic signature extractor grew. Steve's first efforts goaded us into developing something a little more sophisticated. Dave's constant complaints about the functioning of the signature extractor/evaluator have helped to improve its performance greatly. We are also grateful to Greg Sorkin for new insights into how to improve the performance of the signature extraction algorithm, particularly in the case of compiled viruses, and for his invention of many of the automatic virus analysis techniques that will be incorporated into the computer immune system.
1 Unfortunately, this region of the virus is the favorite target of virus-author wannabees because it can enable the new strain to go undetected until a new signature is chosen.
2 Although the algorithm is typically run on an IBM RS/6000 workstation, the code has been ported successfully to OS/2.
[Back to index] [Comments (0)]