Leonard Adleman
Advances in Cryptology - CRYPT0 '88, LNCS 403, pp. 354-374, 1990
1990
 Download PDF (729.53Kb) (You need to be registered on forum)
Download PDF (729.53Kb) (You need to be registered on forum)Research supported by NSF through grant CCR 8519296
In recent years the detection of computer viruses has become common place. It appears that for the most part these viruses have been 'benign' or only mildly destructive. However, whether or not computer viruses have the potential to cause major and prolonged disruptions of computing environments is an open question.
Such basic questions as:
have been at most partially addressed [Col][Co2]1. Indeed a generally accepted definition of computer virus has yet to emerge.
For these reasons, a rigorous study of computer viruses seems appropriate.
For the purpose of motivating the definitions which follow, consider this (fabricated) `case study':
A text editor becomes infected with a computer virus. Each time the text editor is used, it performs the text editing tasks as it did prior to infection, but it also searches the files for a program and infects it. When Tun, each of these newly infected programs performs its `intended' tasks as before, but also searches the files for a program and infects it. This process continues. As these infected programs pass between systems, as when they are sold,OTgiven to others, new opportunities for spreading the virus are created. Finally, after Jan. 1, 1990, the infected programs cease acting as before. Now,each time such a program is run, it deletes all files.
Such a computer virus can easily be created using a program scheme (in an ad hoc language) similar to that found in [Col]:
{main:=
call injure;
...
call submain;
...
call infect;
...
}
{injure:=
if condition then whatever damage is to be done and halt
}
{infect:=
if condition then infect files
}
where for the `case study virus':
{main:=
call injure;
call submain;
call infect;
}
{injure:=
if date ≥ Jan. 1,1990 then
while files ≠ 0:
file = get-random-file;
delete file;
halt;
}
{infect:=
if true then
file = get-random-executable-file;
rename main routine submain;
prepend self to file;
}
By modifying the scheme above, a wide variety of viruses can be created. Even `helpful' viruses may be created. For example the following minor variant of Cohen's [Col] compression virus which saves storage space:
{main:=
call injure;
decompress compressed part of program;
call submain;
call infect;
}
{injure:=
if false then halt
}
{infect:=
if executable-files ≠ 0 then
file = get-random-executable-file;
rename main routine submain;
compress file;
prepend self to file;
}
With the `case study virus' and all of those which could be created by the scheme above, it appears that the following properties are relevant:
A formal definition of computer virus is presented next.
Notation 1
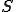 denotes the set of all finite sequences of natural numbers.
denotes the set of all finite sequences of natural numbers. denotes a computable injective function from
denotes a computable injective function from 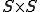 onto
onto 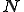 with computable inverse.
with computable inverse.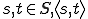 denotes
denotes 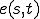 .
.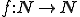 , for all
, for all 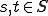 ,
, 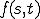 denotes
denotes 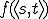 .
.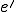 denotes a computable injective function from
denotes a computable injective function from 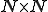 onto
onto 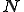 with computable inverse such that for all
with computable inverse such that for all 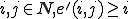 .
.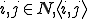 denotes
denotes 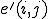 .
.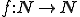 , for all
, for all 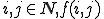 denotes
denotes 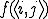 .
.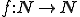 , for all
, for all 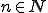 , write
, write 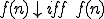 is defined.
is defined.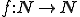 , for all
, for all 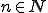 , write
, write 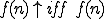 is undefined.
is undefined.Definition 1 For all partial 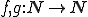 , for all
, for all 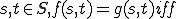 either:
either:
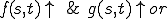
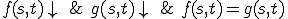
Definition 2 For all 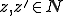 , for all
, for all 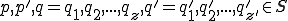 , for all partial functions
, for all partial functions 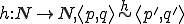 iff:
iff:
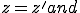
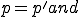
 , with
, with 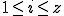 such that
such that 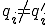 and
and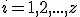 , either
, either
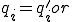
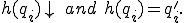
Definition 3 For all partial 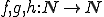 , for all
, for all 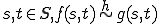 iff
iff 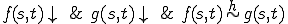 .
.
Definition 4 For all partial 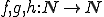 , for all
, for all  iff
iff 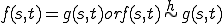 .
.
Definition 5 For all Gödel numberings of the partial recursive functions  , a total recursive function
, a total recursive function  is a virus with respect to
is a virus with respect to  iff for all
iff for all 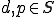 , either:
, either:
![\left(\forall i, j \in N\right)
\left[ \phi_{v(i)}(d, p) = \phi_{v(j)}(d, p) \right]](../img/cache/5b1f9e73745332b4b3c71302cbef99c9.gif)
![\left(\forall j \in N\right)
\left[\phi_j(d, p) \overset{v}{\overset{\sim}{=}} \phi_{v(j)}(d, p)\right]](../img/cache/b26ff7cc546ab7a13c6990b7e321162a.gif)
Remark 1 The choice of symbols 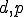 above is intended to suggest the decomposition of all `accessible'information into `data' (information not susceptible to infection) and `programs'(infomation susceptible to infection).
above is intended to suggest the decomposition of all `accessible'information into `data' (information not susceptible to infection) and `programs'(infomation susceptible to infection).
In this section the set of viruses is decomposed into the disjoint union of four principal types. The nature of so called `Trojan horses' is considered.
Definition 6 For all Gödel numberings of the partial recursive functions  , for all viruses
, for all viruses  with respect to
with respect to  , for all
, for all 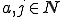 :
:
 is pathogenic with respect to
is pathogenic with respect to  and
and 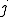 iff
iff
![i = v(j)\ &\\
\left(\exists d, p \in S\right)
\left[\phi_j(d, p) \overset{v}{\overset{\sim}{=}} \phi_i(d, p)\right]](../img/cache/0a96256f617ac2cba1ce2d67d985afb1.gif)
 is contagious with respect to
is contagious with respect to  and
and 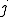 iff
iff
![i = v(j)\ &\\
\left(\exists d, p \in S\right)
\left[\phi_j(d, p) \overset{v}{\sim} \phi_j(d, p)\right]](../img/cache/71939b1222dcad97eecc02bca3d108ba.gif)
 is benignant with respect to
is benignant with respect to  and
and 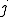 iff
iff
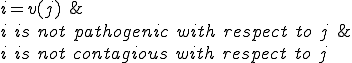
 is a Trojan horse with respect to
is a Trojan horse with respect to  and
and 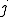 iff
iff
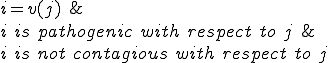
 is a carrier with respect to
is a carrier with respect to  and
and  iff
iff
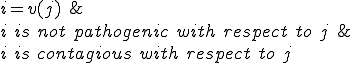
 is virulent with respect to
is virulent with respect to  and
and  iff
iff
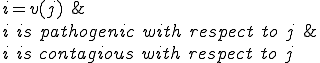
When there exists a unique 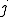 such that
such that 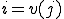 (e.g. when
(e.g. when  is injective) then if
is injective) then if  is pathogenic (contagious, benignant, a Trojan horse, a carrier, virulent) with respect to
is pathogenic (contagious, benignant, a Trojan horse, a carrier, virulent) with respect to  and
and 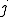 , the reference to
, the reference to 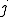 will be dropped and
will be dropped and  will be said to be pathogenic (contagious, benignant, a Trojan horse, a carrier, virulent) with respect to
will be said to be pathogenic (contagious, benignant, a Trojan horse, a carrier, virulent) with respect to  .
.
Hence, if with respect to some virus an infected program is benignant, then it computes the same function as its uninfected predecessor. If it is a Trojan horse then it is incapable of infecting other programs. It can only imitate or injure, and under the right conditions it will do the latter. If it is a carrier, it is incapable of causing injury but under the right conditions it will infect other programs.
Definition 7 For all Gödel numberings of the partial recursive functions  , for all viruses
, for all viruses  with respect to
with respect to  :
:
 is benign iff both:
is benign iff both:
![\left(\forall j \in N \right) \left[ v(j)\ is\ not\ pathogenic\ with\ respect\ to\ v\ and\ j\right]\\
\left(\forall j \in N \right) \left[ v(j)\ is\ not\ contagious\ with\ respect\ to\ v\ and\ j\right]](../img/cache/84c1243a66eb56130fec2710b47a4162.gif)
 is Epeian2 iff both:
is Epeian2 iff both:
![\left(\exists j \in N \right) \left[ v(j)\ is\ pathogenic\ with\ respect\ to\ v\ and\ j\right]\\
\left(\forall j \in N \right) \left[ v(j)\ is\ not\ contagious\ with\ respect\ to\ v\ and\ j\right]](../img/cache/0f19fd75b13862bb80da78181fe23004.gif)
 is disseminating iff both:
is disseminating iff both:
![\left(\forall j \in N \right) \left[ v(j)\ is\ not\ pathogenic\ with\ respect\ to\ v\ and\ j\right]\\
\left(\exists j \in N \right) \left[ v(j)\ is\ contagious\ with\ respect\ to\ v\ and\ j\right]](../img/cache/716e5df14de3054c9bfc598365b69d28.gif)
 is malicious iff both:
is malicious iff both:
![\left(\exists j \in N \right) \left[ v(j)\ is\ pathogenic\ with\ respect\ to\ v\ and\ j\right]\\
\left(\exists j \in N \right) \left[ v(j)\ is\ contagious\ with\ respect\ to\ v\ and\ j\right]](../img/cache/579944f68b7c2a30105c79c241d85ce1.gif)
The next theorem records some simple facts about types of viruses.
Theorem 1 For all Gödel numberings of the partial recursive functions  for all viruses
for all viruses  with respect to
with respect to  :
:
![\left(\exists j \in N\right)\left[v(j)\ is\ benignant\ with\ respect\ to\ v\ and\ j]](../img/cache/e5b64421b1a3e45d27c9a057e8293c64.gif)
 is benign iff
is benign iff
![\left(\forall j \in N\right)\\
\left[v(j)\ is\ benignant\ with\ respect\ to\ v\ and\ j\right]](../img/cache/2a2818129f6f11a5faf6117bf1c38af6.gif)
 is Epeian then
is Epeian then
![\left(\forall j \in N\right)\\
[[v(j)\ is\ benignant\ with\ respect\ to\ v\ and\ j]\ or\\
[v(j)\ is\ a\ Trojan\ horse\ with\ respect\ to\ v\ and\ j]]](../img/cache/59544182333332099468096c66603443.gif)
 is disseminating then
is disseminating then
![\left(\forall j \in N\right)\\
[[v(j)\ is\ benignant\ with\ respect\ to\ v\ and\ j]\ or\\
[v(j)\ is\ a\ carrier\ with\ respect\ to\ v\ and\ j]]](../img/cache/4d892c3bdf5929fcf48b4e9f465d859d.gif)
Proof
Part 1 follows immediately from the recursion theorem.
All other parts follow immediately from the definitions.

Thus, all programs infected by a benign virus are benignant with respect to their uninfected predecessors. They function just as if they had never been infected. Viruses in this class appear to be the least threatening. This class includes many `degenerate' viruses such as the identity function and `padding' functions.
Programs infected by an Epeian virus can only be benignant or Trojan horses with respect to their uninfected predecessors. Further the latter option must sometimes occur. Epeian viruses will not be able to spread themselves; however, an infected program may imitate the `intended' task of its uninfected predecessor until some `trigger' causes it to do damage. Among the Epeian viruses are the `degenerate' class of constant functions, which never imitate-or-infect but only injure.
Programs infected by a disseminating viruses can only be benignant or carriers with respect to their uninfected predecessors. Further the latter option must sometimes occur. Thus programs infected with such viruses are never pathogenic. However, it is worth noting that disseminating viruses may modify the size of programs or their complexity characteristics, and by this means become detectable or cause harm (or benefit as in the case of the compression virus). In fact, size and complexity may be important properties when considering viruses. An extension of the current theory to account for size and complexity seems appropriate (see § further research).
Malicious viruses can both spread and produce injuries. They appear to be the most threatening kind of virus. The `case study virus' in § basic definitions is malicious.
Remark 2 It may be appropriate to view contagiousness as a necessary property of computer viruses. With this perspective, it would be reasonable to define the set of viruses as the union of the set of disseminating viruses and the set malicious viruses, and to exclude benign and Epeian viruses altogether.
The question of detecting viruses is addressed in the next theorem:
Theorem 2 For all Gödel numberings of the partial recursive functions 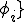 :
:
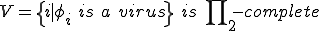
Proof
Let 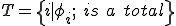 . It is well known (§13 and §14 [Ro]) that
. It is well known (§13 and §14 [Ro]) that 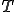 is
is 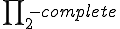 .
.
To establish that 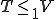 , let
, let 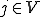 (for examplelet
(for examplelet 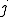 be an index for the identity function) and consider the function
be an index for the identity function) and consider the function 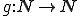 such that for all
such that for all 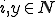 :
:
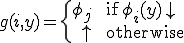
Then 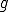 is a partial recursive function. Let
is a partial recursive function. Let 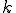 be an index for
be an index for 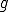 , and let
, and let  , be such that:
, be such that:
![\left(\forall i \in N\right)
\left[f(i) = s(k, 1, i)\right]](../img/cache/be2250e6350719e518057555fb3344b2.gif)
where  is as in the
is as in the 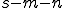 theorem [Ro].
theorem [Ro].
Then 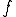 is a total recursive function and:
is a total recursive function and:
![\left(\forall i, y \in N\right)
[
\phi_{f(i)}(y) = \phi_{s(k,1,i)}(y) = \phi_k(i,y) = g(i,y) =
\{
\begin{eqnarray}
{\phi_j(y)} && \text{if }\phi_i(y)\downarrow\\
{\uparrow} && \text{otherwise}
\end{eqnarray}
]](../img/cache/16bb0c63be5614d8add2a230fd2226e6.gif)
It follows that
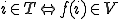
Thus 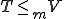 . It follows, as in §7.2 [Ro], that
. It follows, as in §7.2 [Ro], that 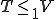 as desired.
as desired.
To establish that 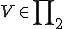 , consider the following formula for
, consider the following formula for 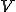 which arises directly from the definition of virus:
which arises directly from the definition of virus:
![\begin{eqnarray}
(\forall j)(\exists k, t) && [H(i,j,k,t)]\\
\&\\
(\forall \langle d, p \rangle) && [\forall j_1, k_1, t_1)\\
&& [H(i,j_1,k_1,t_1) \Right\\
&& (\forall\langle e, q\rangle,t_2)
[\neg H(k_1,\langle d, p\rangle,\langle e, p\rangle, t_2)]] \\
&& or\\
&& (\forall j_1,k_1,t_1,j_2,k_2,t_2)\\
&& [[H(i,j_1,k_1,t_1) \& H(i,j_2,k_2,t_2)] \Right\\
&& (\exists \langle e, q \rangle, t_3, t_4) \\
&& [H(k_1,\langle d, p\rangle,\langle e, q\rangle, t3) \& \\
&& H(k_2,\langle d, p\rangle,\langle e, q\rangle, t4)]] \\
&& or \\
&& (\forall j_1,k_1,t_1, langle e, q \rangle, t2)\\
&& [[H(i,j_1,k_1,t_1) \&
H(j_1,\langle d, p \rangle, \langle e, q \rangle, t_2)] \Right \\
&& (\exists \langle e', q' \rangle, t_3, t_4) \\
&& [H(k_1, \langle d, p \rangle, \langle e', q' \rangle, t_3) \& \\
&& L(i, \langle e, q \rangle, \langle e', q' \rangle, t_4)] \\
&& \& \\
&& [H(i,j_1,k_1,t_1) \&
H(k_1, \langle d, p \rangle, \langle e, q \rangle, t_2)] \Right \\
&& (\exists \langle e', q' \rangle, t_3, t_4) \\
&& [H(j,\langle d, p \rangle, \langle e', q' \rangle, t_3) \& \\
&& L(i,\langle e', q' \rangle, \langle e, q \rangle, t_4)]]]
\end{eqnarray}](../img/cache/d3857efa44d1a0e7dd0227721f4d3672.gif)
Where 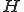 is a `step counting' predicate for
is a `step counting' predicate for  such that:
such that:
![(\forall i,j,k)\\
\text{if }\phi_i(j) = k \text{then } (\exists t)[H(i,j,k,t)]\\
\text{if }\phi_i(j) \ne k \text{then } (\forall t)[\neg H(i,j,k,t)]](../img/cache/42f8aa3a4a0edca2467c336f16e1af4d.gif)
And where 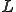 is a predicate for
is a predicate for  such that:
such that:
![(\forall i, \langle e, q \rangle, \langle e', q' \rangle, t)\\
\text{if } \langle e, q \rangle \overset{\phi_i}{\sim} \langle e', q' \rangle \text{then }(\exists t)[L(i, \langle e, q \rangle, \langle e', q' \rangle, t)]\\
\text{if } \langle e, q \rangle \overset{\phi_i}{\not\sim} \langle e', q' \rangle \text{then }(\forall t)[\neg L(i, \langle e, q \rangle, \langle e', q' \rangle, t)]](../img/cache/21df2c285ea69225ebd96c0bd1d589c1.gif)
Since for all acceptable Gödel numberings of the partial recursive functions  it is easily seen that there exist recursive predicates
it is easily seen that there exist recursive predicates 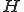 and
and 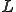 as above, it follows that
as above, it follows that 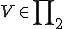 .
.

Thus detecting viruses is quite intractable, and it seems unlikely that protection systems predicated on virus detection will be successful.
As noted in [Co1] isolating a computing environment from its surroundings is a powerful method of protecting it from viruses. For example, if no new programs can be introduced, no old programs can be updated, and no communication can occur, then it seems viruses are no threat.
Unfortunatly, such isolation is unrealistic in many computing environments. The next theorems explore the possibility of protecting computing environments with less severe forms of isolation.
Definition 8 For all Gödel numberings of the partial recursive functions  , for all viruses
, for all viruses  with respect to
with respect to  , let:
, let:
The infected set of 
![I_v = \{i \in N|(\exists j \in N)[i= v(j)]\}](../img/cache/04d7f924de23c242f1cfbe1477b032b4.gif)
Definition 9 For all Gödel numberings of the partial recursive functions  , for all viruses
, for all viruses  with respect to
with respect to  ,
,  is absolutely isolable iff
is absolutely isolable iff 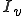 is decidable.
is decidable.
Clearly if a virus is absolutely isolable, then (at least in theory) it can be neutralized. Whenever a program becomes infected, it is detected and removed. The following is a simple fact about absolutely isolable viruses:
Theorem 3 For all Gödel numberings of the partial recursive functions  , for all viruses
, for all viruses  with respect to
with respect to  if for all
if for all 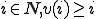 then
then  is absolutely isolable.
is absolutely isolable.
Proof trivial.

Thus the case study virus, as implemented using the scheme in §basic definitions would be absolutely isolable. In fact, what little experience with viruses there is to date seems to suggest that in practice people who produce viruses begin by producing ones with the increasing property necessary for theorem 3 to apply. Unfortunately, not all viruses have this property. For example, with any reasonable compression scheme, the compression virus of §basic definitions would not have this property. Nonetheless, the compression virus is absolutely isolable. Given a program with the proper syntax, it is in the infected set if and only if decompressing the compressed part results in a legitimate program.
Is every virus absolutely isolable?
Regretably, the next theorem shows that the answer is no.
Theorem 4 For all Gödel nurnberings of the partial recursive functions  , there exists a total recursive function
, there exists a total recursive function  such that:
such that:
 is a malicious virus with respect to
is a malicious virus with respect to 
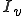 is
is 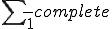 .
.Proof
Let 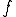 be a total recursive function such that:
be a total recursive function such that:
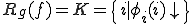
Let 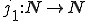 be a 1 - 1 total recursive function such that for all
be a 1 - 1 total recursive function such that for all 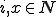 :
:

Such a function, known as a padding function, exists by Proposition 3.4.5 [MY].
Let 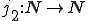 be such that:
be such that:
![(\forall i, x \in N)[j_2(i, x) = j_1(i, y)]](../img/cache/f814c621b19d17199d8f56e7e3748cf6.gif)
where 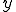 is the least natural number such that, for all
is the least natural number such that, for all 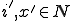 with
with 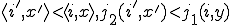 .
.
Then 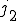 is a monotonically increasing total recursive function and by (1), it follows that:
is a monotonically increasing total recursive function and by (1), it follows that:
![(\forall i, x \in N)[\phi_i = \phi_{j_2(i, x)}] \hspace{100}(2)](../img/cache/29494b26887f90ff8cc5f51cb128c19c.gif)
Let 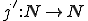 be such that for all
be such that for all 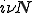 :
:
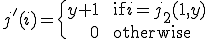
Then since 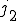 is monotonically increasing, it follows that
is monotonically increasing, it follows that 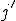 is a total recursive function.
is a total recursive function.
Consider the function 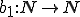 such that for all
such that for all 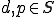 and
and 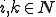 :
:
![\phi_{b_1(i, k)}(d, p) = \{
\begin{eqnarray}
0 && \text{if } d \text{ is even} \\
\langle e, [\phi_k(q)] \rangle && \text{if } d \text{ is odd } \& \phi_i(d, p) = \langle e, [q] \rangle \text{ and } \phi_k(q)\downarrow \\
\uparrow && \text{if } d \text{ is odd } \& \phi_i(d, p) = \langle e, [q] \rangle \text{ and } \phi_k(q)\uparrow \\
\phi_i(d, p) && \text{otherwise}
\end{eqnarray}](../img/cache/97961fe1511c89604e822a21a3931dd5.gif)
where for all 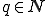 ,
, ![[q]](../img/cache/fc15bc3e2889ee6f5797eb3588669007.gif) denotes the one element sequence in
denotes the one element sequence in 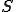 consisting only of
consisting only of 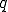 .
.
Then by standard arguments, 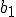 is a total recursive function and:
is a total recursive function and:
![(\forall i, x, k \in N)[\phi_{b_1(i, k)} = \phi_{b_1(j_2(i, x), k)}]. \hspace{100}(3)](../img/cache/c144991e849a9d26df2406db79d2c5e4.gif)
Let 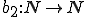 be such that for all
be such that for all 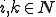 :
:
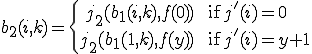
Then 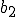 is a total recursive function and it follows from (2) and (3) that:
is a total recursive function and it follows from (2) and (3) that:
![(\forall i, k \in N)[\phi_{b_2(i, k)} = \phi_{b_1(i, k)}]. \hspace{100}(4)](../img/cache/d794b21b2989f327d84ec92da6c5b80c.gif)
Applying the s-m-n theorem there exists a total recursive function 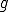 such that for all
such that for all 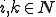 :
:
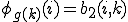
By the recursion theorem, there exists an 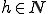 such that for all
such that for all 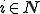 :
:
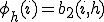
Let 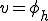 . Then
. Then  is a total recursive function since
is a total recursive function since 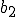 is.
is.
Let 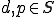 , then using that fact that
, then using that fact that 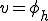 is a total recursive function and applying (4) gives:
is a total recursive function and applying (4) gives:
![\begin{eqnarray}
\phi_{v(i)}(d, p) &=& \phi_{b_2(i, h)}(d, p)\\
&=& \phi_{b_1(i, h)}(d, p)\\
&=& \{
\begin{align}
0 && \text{if }d \text{ is even} \\
\langle e, [\phi_h(q)]\rangle && \text{if }d \text{ is odd } \binampersand \phi_i(d, p) = \langle e, [q] \rangle \binampersand \phi_h(q)\downarrow\\
\uparrow && \text{if }d \text{ is odd } \binampersand \phi_i(d, p) = \langle e, [q] \rangle \binampersand \phi_h(q)\uparrow\\
\phi_i(d, p) && \text{otherwise}
\end{align} \\
&=& \{
\begin{align}
0 && \text{if }d\text{ is even}\\
\langle e, [v(q)]> && \text{if }d\text{ is odd} \binampersand \phi_i(d, p) = \langle e, [q] \rangle\\
\phi_i(d, p) && \text{otherwise}
\end{align}
\end{eqnarray}](../img/cache/ae3d53643ca33f859a1fb6d101d1f778.gif)
1 of the theorem now follows directly from the definition of malicious virus.
Since, for all total recursive functions 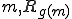 is recursively enumerable, it follows that
is recursively enumerable, it follows that 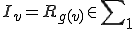 .
.
Let 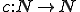 be such that for all
be such that for all 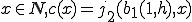 . Since
. Since 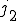 is 1 - 1 so is
is 1 - 1 so is  . Then
. Then 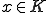 implies the existence of a
implies the existence of a 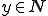 such that
such that 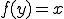 . Let
. Let 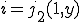 , then:
, then:
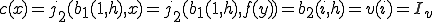
On the other hand, assume 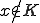 and
and 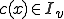 . Then there exists an
. Then there exists an 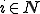 such that:
such that:
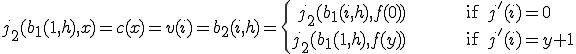
Since 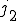 is 1 - 1, it follows that
is 1 - 1, it follows that 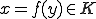 .
.  . Hence,
. Hence, 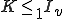 and 2 of the theorem holds.
and 2 of the theorem holds.

Thus, for the viruses described in the previous theorem, protection cannot be based upon deciding whether a particular program is infected or not. Paradoxically, despite this, it is often possible to defend against such viruses. How such a defense could be mounted will be described below; however, a few definitions are in order first.
Definition 10 For all Gödel numberings of the partial recursive functions  , for all viruses
, for all viruses  with respect to
with respect to  , let:
, let:
The germ set of 
![G_v = \{ i|i \in N & (\exists j \in N)[\phi_i = \phi_{v(j)}]\}](../img/cache/0a9e4bd468e62d9147e2a251a88f1ded.gif)
Thus the germs of a virus are functionally the same as infected programs, but are syntactically different. They can infect programs, but cannot result from infection. They may start `epidemics', but are never propagated with them.
Definition 11 For all Gödel numberings of the partial recursive functions  , for all virzlses
, for all virzlses  with respect to
with respect to  ,
,  is isolable within its germ set iff there exists an
is isolable within its germ set iff there exists an 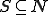 such that:
such that:
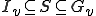 .
.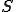 is decidable.
is decidable.Notice that if a virus is isolable within its germ set by a decidable set 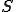 , then not allowing programs in the set
, then not allowing programs in the set 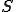 to be written to storage or to be communicated will stop the virus from infecting. Further, the isolation of some uninfected germs by this process appears to be an added benefit.
to be written to storage or to be communicated will stop the virus from infecting. Further, the isolation of some uninfected germs by this process appears to be an added benefit.
Returning now to the viruses described in the previous theorem: assume that the function 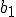 above had the property that for all
above had the property that for all 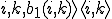 . The proof of the previous theorem could easily have been modified to assure this. Further, in Godel numberings derived in the usually fashion from natural programming languages, a
. The proof of the previous theorem could easily have been modified to assure this. Further, in Godel numberings derived in the usually fashion from natural programming languages, a 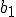 constructed in a straightforward manner would have this property. Consider the set
constructed in a straightforward manner would have this property. Consider the set
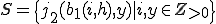
By the monotonically increasing property of 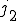 and the property of
and the property of 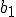 which is being assumed,
which is being assumed, 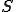 is decidable. On the other hand if
is decidable. On the other hand if 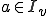 then there exists
then there exists  such that
such that
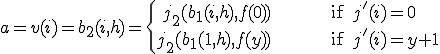
And it follows that 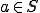 . On the other hand if
. On the other hand if 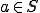 then there exist an
then there exist an 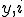 such that
such that
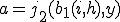
By (2) and (4):
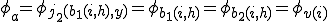
And hence 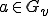 as desired.
as desired.
Thus viruses like the ones in theorem 4 demonstrate that decidability of 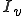 is sufficient but not necessary for neutralization. Apparently, more work needs to be done before a clear idea of the value of isolation will emerge. Are all viruses isolable within their germ set? The answer is no (proof omitted). Are all disseminating viruses isolable within their germ set? The answer is not known. Are there notions of isolation which provide significant protection at a reasonable cost?
is sufficient but not necessary for neutralization. Apparently, more work needs to be done before a clear idea of the value of isolation will emerge. Are all viruses isolable within their germ set? The answer is no (proof omitted). Are all disseminating viruses isolable within their germ set? The answer is not known. Are there notions of isolation which provide significant protection at a reasonable cost?
The study of computer viruses is embryonic. Since so little is known, virtually any idea seems worth exploring.
Listed below are a few avenues for further investigation.
Introduce complexity theory and program size theory into the study of computer viruses. As noted earlier, even disseminating viruses may affect the complexity characteristics and size of infected programs and as a result become detectable or harmful.
Complexity theory and program size considerations can be introduced at a abstract level (see for example [MY]) or a concrete level.
For example, viruses in the `real world' would probably have the property that the running time of an infected program, at least while imitating or infecting, would be at most polynomial (linear) in the running time of its uninfected precursor. Does this class of `polynomid (linear) viruses' pose a less serious threat? Do NP-completeness considerations, or cryptographic considerations come into play?
In this paper one form of protection mechanism, isolation, was briefly considered. In addition to considering isoIation in greater depth, numerous other possibilities exist. For example:
The notion of computer viruses presented here is not the only one possible. It was selected because it seemed to be art adequate place to begin an investigation. More general, and more restrictive notions are possible. Indeed it seems possible that no definition will conform to everyone's intuitions about `computer viruses'.
More `machine dependent' approaches could be considered. Approaches which take into account the communications channels over which viruses pass seem particularly important.
One interesting generalization of the current notion is inspired by [Co1], where viruses are assumed to be capable of evolving. The `Mutating Viruses' (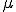 -viruses) partially defined next are an attempt to capture this property.
-viruses) partially defined next are an attempt to capture this property.
Definition 12 For all 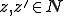 , for all
, for all 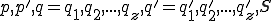 , for all sets
, for all sets 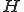 of partial functions from
of partial functions from 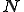 to
to 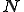 ,
, 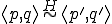 iff:
iff:
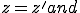
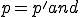
 , with
, with 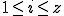 such that
such that 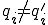 and
and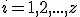 , either
, either
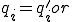
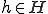 such that
such that 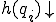 and
and 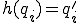 .
.Definition 14 For all sets of partial functions 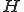 from
from 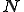 to
to 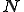 , for all partial
, for all partial 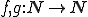 , for all
, for all 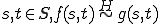 iff
iff 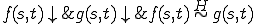 .
.
Definition 15 For all Gödel numberings of the partial recursive functions  a set
a set 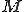 of total recursivefunctions is a mutating virus,
of total recursivefunctions is a mutating virus, 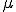 -virus, with respect to
-virus, with respect to  iff both:
iff both:
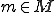 , for all
, for all 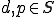 either:
either:
![(\forall i, j \in N)[\phi_{m(i)}(d, p) = \phi_{m(j)}(d, p)]](../img/cache/5875bbbf38c273f8db0ff4cb480109c7.gif)
![(\forall j \in N)[\phi_j(d, p) \overset{M}{\overset{\sim}{=}} \phi_{m(j)}(d, p)]](../img/cache/7a70f7d5a60a143f038e3bafdc9298a5.gif)
Some computer viruses which have recently caused problems (e.g. the so called `Scores virus' [Up] which attacked Macintosh computers) are 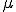 -viruses and not just viruses. Hence this generalization of the notion of virus may be of more than theoretical interest.
-viruses and not just viruses. Hence this generalization of the notion of virus may be of more than theoretical interest.
This is only a partial definition because some notion of `connectivity' is needed. That is, the union of two 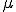 -viruses, neither of which `evolves' into the other should not be a
-viruses, neither of which `evolves' into the other should not be a 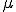 -virus. Many definitions of `connectivity' can be defined, but further study will be required to choose those which are most appropriate. Once an appropriate choice is made, an important question will be whether the set of infected indices of a
-virus. Many definitions of `connectivity' can be defined, but further study will be required to choose those which are most appropriate. Once an appropriate choice is made, an important question will be whether the set of infected indices of a 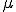 -virus can be harder to detect than those of a virus.
-virus can be harder to detect than those of a virus.
This issue has evolved during joint work with K. Kompells.
There appear to be programs which can reproduce or reproduce and injure but which are not viruses (e.g. programs which just make copies of themselves but never `infect'). These `computer organisms' may be a serious security problem.
It may be appropriate to study `computer organisms' and treat `computer viruses' as special case.
I would like to thank Dean Jacobs, and Gary Miller for contributing their ideas to this paper.
I would also like to thank two of my students: Fred Cohen and Kireeti Kompella. Cohen brought the threat of computer viruses to my (and everyone's) attention. Kompella has spent many hours reviewing this work and has made numerous suggestions which have improved it.
1 It appears that F. Cohen is the first researcher in an academic setting to consider the practical and theoretical aspects of computer viruses. The formalism presented here differs considerably from that explored by Cohen [Col][Co2].
2Now rhift your theme, and ring that wooden horse
Epeior built, inrpired by Athena -
the ambuscade Odysseus filled with fighters
and rent to take the inner town of troy
The Odyssey of Homer, 8.492-495.
translation by Robert Fitzgerald
Doubleday & Co.,NY, 1961