Philippe Beaucamps
International Conference on Computer, Electrical, and Systems Science, and Engineering - CESSE'07
November 2008
Download PDF (310.73Kb) (You need to be registered on forum)Nowadays viruses use polymorphic techniques to mutate their code on each replication, thus evading detection by antiviruses. However detection by emulation can defeat simple polymorphism: thus metamorphic techniques are used which thoroughly change the viral code, even after decryption. We briefly detail this evolution of virus protection techniques against detection and then study the METAPHOR virus, today’s most advanced metamorphic virus.
Keywords Computer virus, Viral mutation, Polymorphism, Metamorphism, MetaPHOR, Virus history, Obfuscation, Viral genetic techniques
WHen the first antiviral protections appeared in the late 80’s to answer the nascent viral threat, they consisted of a mere binary scan of programs looking for known virus signatures. Never mind, virus writers adapted their code so that it would mutate its binary form on each replication: as early as in 1988 a first virus protected itself using encryption, followed in 1990 by the first polymorphic viruses which were able to mutate their code as well as their decryption method. Their ability to evade detection by the then antivirus software gave them immediate “popularity”. Nevertheless antiviruses quickly adapted to this protection by letting viruses decrypt themselves and then only scanning the decrypted code looking for any known signature. This led, as early as in 1997, to the first metamorphic viruses which mutate their code in its decrypted form.
This article will therefore study polymorphism and its miscellaneous techniques and more particularly the most evolved ones, namely metamorphic techniques. In order to do so, we will study most notably the 2002 METAPHOR virus. For more details, the reader may consult ´Eric Filiol’s books [Fil05], [Fil07] as well as the VX Heavens website, which is crammed with malware resources.
This section shortly describes the evolution and techniques of viruses from the most basic techniques to simple polymorphic techniques and finally to advanced metamorphic techniques. The reader may refer to [Fil05], [Fil07], [Szo05], [Ayc06] for a more exhaustive and detailed study.
The first virus outbreak broke out in 1981 with the ELK CLONER virus, followed by BRAIN in 1986, the first virus to implement stealth techniques, and from then by numerous other viruses. The most commonly used techniques consisted in appending the viral code at the end of the executable file, modifying the entry point to point at the virus and then letting the virus spread among the system (fig. 1). Thus, a basic protection method is form analysis where each virus is identified by a specific signature: such a signature is a sequence of – not necessarily consecutive – bytes whose detection inside a program allows to identify as undeniably as possible infection by the virus. This method has the advantage of being non-greedy in its complexity as well as subject to a tiny rate of false alarms.
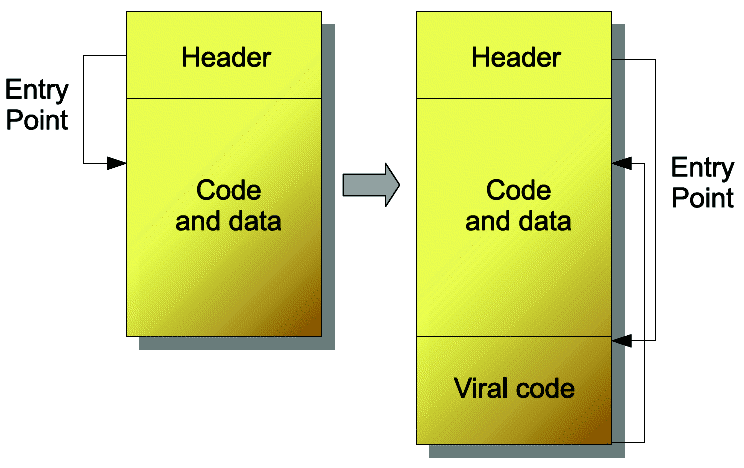
Fig. 1. Basic virus infection.
Back in time, as early as in 1984, F. Cohen had been the first one to study viruses from a theoretical point of view, christening them and defining them as programs which are able to infect other programs with a possibly evolved copy of themselves. Thus, this definition already suggested the existence of viruses which would alter their form when replicating. And indeed such viruses turned up quite quickly. Cohen also showed that the problem of virus detection was undecidable, meaning in other words that no algorithm would ever be able to determine with unquestionable certainty whether a given program is a virus or not [Coh84].
The first virus encrypting its code, CASCADE, appeared in 1988. Yet its decryption method remained unchanged from one replication to another and thus it was not really a polymorphic virus per se. In 1990 however, the first family of polymorphic viruses appeared: the CHAMELEON viruses (or V2P) which were developped by Mark Washburn, were based on the CASCADE and VIENNA viruses and mutated the code of their decryption method (fig. 2). The shock they created shaked the antiviral community, since detection techniques using a fixed signature had suddenly become obsolete for this new brand of viruses.
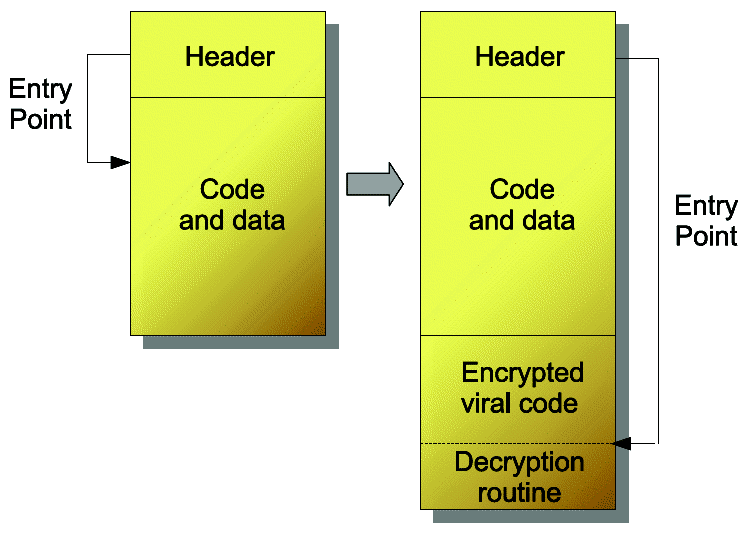
Fig. 2. Polymorphic virus infection.
The famous WHALE virus appeared the same year: it included polymorphism, stealth and armouring techniques and mutated in particular the code of its mutation function using obfuscation techniques (dead code, test repetition, redundant code, ...). Then “boards” appeared, where were shared viruses and e-zines, among which Phrack and 40Hex, and where were worked out and shared new viral techniques. Then in 1992 the first polymorphic engines appeared, like MTE, TPE, NED and DAME1, which could be linked to the virus to produce a polymorphic variant. They were quickly followed by the first virus creation toolkits, like VCL, PS-MPC and G22, some of which including polymorphism features. This signalled the start of massive creation – in thousands – of simple and polymorphic viruses.
On the antiviral community side, the answer came in 1992 when Eugene Kaspersky worked out a technique now used by most antivirus products, namely detection by code emulation. Since one could not anymore rely on the static version of a program’s code to detect a virus, the code was run in a controlled (emulated or sandboxed) environment on a given number of instructions, and periodically or in the end the affected memory was analysed to detect the (possibly partially) decrypted viral code. Indeed, and this is the base principle of metamorphism, polymorphic codes had the major drawback of always decrypting themselves into the memory into an invariant and thus detectable form. However this detection technique also has the disadvantage of being quite cpu-intensive.
Several techniques, called anti-emulation techniques, have been developped as a result by virus writers to hinder this kind of detection:
These techniques are detailed in the literature [Fil05], [Fil07], [Ayc06]: some of these techniques are used by METAPHOR and we shall come back on them in the next section.
Finally, we state Spinellis’s recent result [Spi03], which establishes the general complexity of the detection of such viruses. He shows that the problem of detecting polymorphic viruses, of bounded length, is NP-complete, by reducing to it the well-known SAT problem of satisfiability.
Metamorphic viruses are in a sense advanced polymorphic viruses: on each replication, the code to be executed completely mutates, without altering its functionality. Thus, encryption is not anymore necessary and, when used, the decryption method as well as the decrypted code of the virus are different for each new generation. Figure 3 presents a basic example of infection by a metamorphic virus, on its ieme mutation: in practice, the code is often encrypted and the decryption routine is sometimes scattered among the host’s code (ZMIST virus for instance).
The first metamorphic techniques made their appearance in 1997 with the TINY MUTATION COMPILER (TMC), by Ender. This virus had a compiler embedded in its body as well as its own sources in encrypted pseudocode. On execution, the virus decrypted its source code, inserted dead code, mixed up its code and data, and recompiled everything.
On the same year, Z0mbie developped his Z0MBIE’S CODE MUTATION ENGINE (ZCME), which did not use any encryption techniques but allocated a 16K buffer where it randomly copied out its instructions, linking them with each other with JMP instructions and filling the remaining space with dead code.
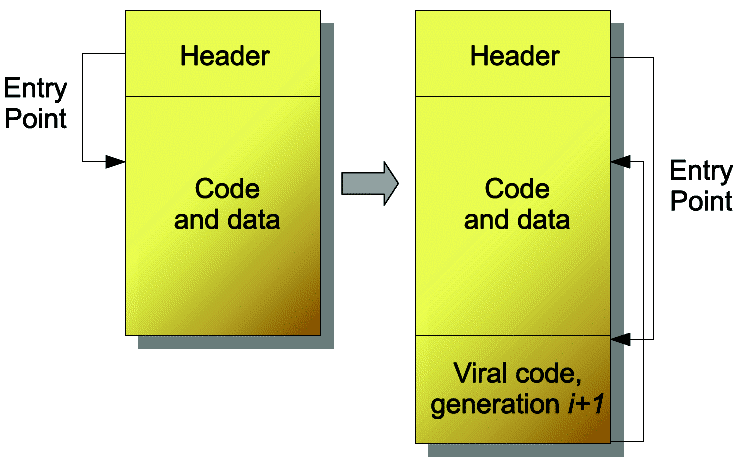
Fig. 3. Metamorphic virus infection on generation i.
In 1998, Vecna implemented MISS LEXOTAN, which disassembled itself, added some dead code and modified the form of its instructions, in a computational way most particularly (see later). To create dead code, it inserted most notably meta-instructions XOR ebp, imm, with no effect, but which defined which registers were used and thus should not be modified. He also implemented REGSWAP later, which shuffled the registers. Here is an excerpt from LEXOTAN:
After transformation, this code may look like this, with no jumps:
In 2000, the BADBOY, ZMORPH, EVOL, ZPERM, BISTRO and ZMIST viruses enter the growing list of metamorphic viruses, using more or less complex techniques. ZPERM most notably introduces the REAL PERMUTATION ENGINE (RPME), which can be linked to other viruses, and enables random permutation of the virus code, with insertion of dead code and branching using JMP instructions.
ZMIST, by Z0mbie, is more particularly one of the most evolved (and most stable) metamorphic viruses until now. It uses the following techniques:
The virus is analysed, along with other polymorphic and metamorphic viruses, in [Szo05].
Finally, METAPHOR, by Mental Driller, appears in 2002 and is certainly the most advanced metamorphic virus until today. It may infect both Elf (on Linux) and PE (on Windows) files, on the local file system and on mounted partitions (in Linux) or shared folders (in Windows).
Let’s also mention the recent development of Java and MSIL3 viruses, which are platform-independent. .NET assemblies infection is simplified by the presence of assembler libraries (System.Reflection.Emit namespace) and both technologies enclose standard high level cryptography libraries. Only one metamorphic MSIL virus is known as of today, —Gastropod—, and there still are very few Java and MSIL viruses. But given the ubiquity of both technologies, these viruses might well represent a threat in the near future for any platform that supports them.
The rapid evolution of viral techniques towards first polymorphic and then metamorphic techniques motivated the working out of new detection techniques, based on emulation and behaviour analysis allowing to identify suspect behaviours. However in the same time, they revealed two limitations that are inherent to antiviral defence and benefit virus writers. First, the efficiency of these methods relies on an often prohibitive complexity when iterated on a high number of files: defence cannot monopolize resources of the protected system whereas attack has a priori no cost nor time limits. Moreover a delay of a few hours or of a day is long enough for a well-implemented virus to spread on a very large scale, hence the interest for virus writers to complicate as much as possible analysis of their viruses. Although these weaknesses, combined with advanced metamorphic techniques, are not used yet in a lot of viruses (or these very viruses are often buggy and easily detected and stopped), they define a new age of viral detection, in which current protection methods will be thoroughly obsolete.
The cross-platform metamorphic virus METAPHOR4 was written in 2002 by The Mental Driller and was the second highly advanced metamorphic virus (with ZMIST), and the first ever polymorphic, and metamorphic, Linux virus. It was published in 29A’s magazine [MD02]: its sources can be found on VX Heavens [MDa]. It uses highly advanced metamorphic techniques which combine the majority of the techniques used by its predecessors. They’re used along with anti-heuristic and anti-emulation techniques.
Here are the main polymorphic techniques used by METAPHOR:
1) Encryption techniques: First let’s describe the miscellaneous encryption techniques which are commonly used in polymorphic viruses (see [Mid99] for some more details and for examples).
a) Basic encryption: The most simple ones, as well as the most common ones, use a mere XOR (as shown in the example), ADD or SUB encryption, with a key which is randomly generated on each replication and which is stored inside the virus data or directly inside the decryption method. The following code is a basic example of such an encryption:
b) Sliding key encryption: One drawback of the previous technique is that, once the key has been chosen, each character is encrypted in a unique way. Thus the sliding key encryption updates the key as the decryption progresses, either in a fixed way or for instance with the last encrypted character. For instance, the previous code could be modified in the following way:
c) Flow encryption: This method uses a key to generate a keystream of the same size as the data to encrypt. For instance the generation of this pseudo-random keystream might use one or several linear feedback shift registers (LFSR, see section III-D1). Some basic implementations simply duplicate as much as needed the input key. The previous code can be easily adapted to this technique, in the case of a single register (lfsr_init initializes the register, and lfsr_next shifts the 32bits register, thus generating a new key):
d) Encryption with permutation: The input data is simply permutated. Permutation can occur on the scale of the whole data, of chunks of bytes (of fixed or variable length), or even of each byte (with the ROR instruction for instance).
e) Multiple encryption: Several encryption techniques are sequentially applied.
f) Random key encryption: The data is encrypted with a random key which is not stored for future decryption. Upon execution, the key (as well as the encryption technique) can only be recovered by brute force attack or cryptanalysis. This technique disables any code emulation analysis. The size of the key space (and possibly its properties) allows to control over the decryption time. This technique was introduced by DarkMan in 1999 in his RANDOM DECODING ALGORITHM ENGINE (RDAE), which implemented several encryption techniques without storing the key: only the code’s CRC32 checksum was stored. These techniques are detailed in [BF07], [Kha07].
g) Code-dependent encryption: The binary code itself is used as the encryption key, or a combination of the code and a random key. This technique was usually used to ensure that the code had not been modified – during an antiviral analysis (where the code could be patched to disable some anti-debugging techniques).
Upon decryption, the virus needs access to the decryption key(s). This key is usually directly stored in the program: inside the decryption procedure, inside the virus data or simply related to the host program (for instance the key can be the host’s filename). The case of RDA is different since the key is retrieved by brute force. However other scenarios exist where the key isn’t stored in the code but is inferred from the environment. This technique is called environmental key generation [RS98]. Here are some examples:
The most advanced implementation of this technique is the proof of concept BRADLEY virus [Fil04]. It uses several encryption layers, whose keys are retrieved from the environment. The interest of such viruses from their writer’s point of view, is that they can restrict the activity of their virus geographically as well as temporally. Filiol also shows in [Fil04] that, if the key is unknown during the analysis, the cryptanalysis’s complexity is exponential (in BRADLEY’s case).
As for METAPHOR, it encrypts its code with an initial probability of 15/16 and uses an encryption method (with random key) of type XOR, ADD or SUB.
However, METAPHOR’s decryption method is much more interesting. It uses techniques that The Mental Driller had already implemented into the TUAREG engine (TAMELESS UNPREDICTABLE ANARCHIC RELENTLESS ENCRYPTION GENERATOR) and that he describes in another issue of 29A’s magazine [MD00], [MDb]. This engine combined most notably two novel techniques, with an anti-heuristic purpose, which also took part in the mutation of the decryption routine. Both techniques, the branching technique and the PRIDE technique, are used in METAPHOR. Finally, an EPO technique is used to give control to the decryption routine: METAPHOR changes all calls to the exit function into calls to this routine. Thus, the virus only gains control after execution of the program, which contributes to its stealth and protects it from the detection by emulation.
2) Branching technique: A basic decryption method has a structure that often follows a common template which will trigger an alarm in any heuristic engine, as one can see with the examples from last section. Thus the branching technique allows to simulate as much as possible the behaviour of an innocuous program. Such programs will usually sequentially test several conditions and, depending on the result, finally branch on distinct paths. This technique therefore creates several random tests, until a given recursivity level, that will define an execution tree with leaves representing distinct ways to decrypt the code. Figure 4 describes the execution tree for a maximum depth of recursivity equal to 2: each terminal branch has its own decryption code, though the final result is the same, whatever branch is taken. Thus for a depth of recursivity equal to n,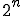 
decryption branches are generated.
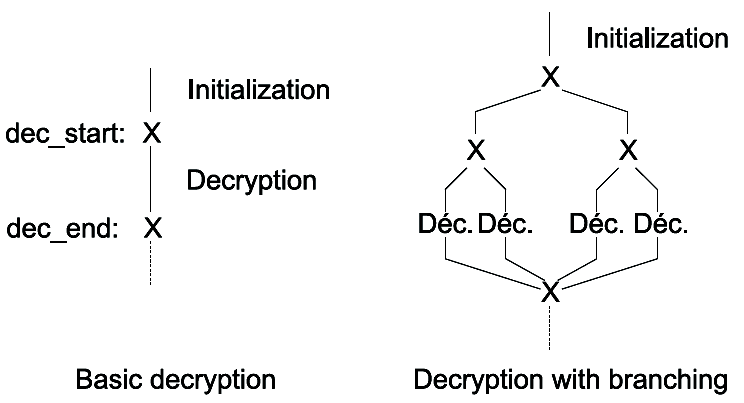
Fig. 4. Execution tree with and without branching technique.
Furthermore, to reduce the risk of an heuristic alert upon execution of a branch, terminal branches do not contain a decryption loop but only its body: once the body is executed, a jump is made to any one of the previous nodes in order to carry on decryption. Thus, upon execution, each branch makes the same computation and all branches are shared and alternatively used to implement the decryption loop. Here is the C algorithm used in METAPHOR (ll. 15750 – 16075):
And here is an example code it could yield, for a recursivity depth of 2:
As this will be detailed in section III-C about metamorphic techniques, this code is actually an intermediate representation of the final code: once the code has been created, METAPHOR generates the final x86 code by rewriting each instruction into an equivalent sequence of instructions and by randomly inserting dead code.
3) PRIDE technique (Pseudo-Random Index DEcryption): The purpose of this technique is also to protect the virus from a heuristic detection. Indeed, even with the modification of the execution tree of the decryption procedure, it follows the following common mechanism (for a basic encryption):
The second stage of this procedure, which consists in sequentially reading a sequence of 1000 bytes or more in memory, presents a high risk of heuristic alert. Therefore, the PRIDE technique consists in decrypting data in a pseudorandom order and not anymore in a sequential order. Byte 10 will be decrypted, then byte 23, then byte 7, then byte 48, and so on. This memory access profile is much closer to an innocuous application’s memory access profile. In the same time, this technique reinforces the polymorphism of the decryption code.
Here is the algorithm used for the PRIDE technique (ll. 15570 – 15652 and 15827 – 15984). size_of_data is the size of the data to be encrypted, rounded up to a power of 2. First the algorithm initializes its variables:
Then it initializes the registers to be used by the decryption routine: CR, IR and BR. CR is the counter register and contains the sequential decryption index, IR is the index register and contains the pseudo-random decryption index (XOR’ed actually with CR), BR is the buffer register used as temporary storage for encrypted data. Compared to the decryption routine in section III-B1, we have: CR ≡ ecx, IR ≡ esi ≡ edi and BR ≡ eax. The following code is written at the beginning of the decryption routine:
Finally, when the decryption routine’s body must be generated (call to insert_code inside the make_branch method), the algorithm writes:
Furthermore, the last instructions which update registers CR and IR (ADD CR, val and AND CR, val’ for the CR register) are permutated with each other, with the obvious requirement that the AND instruction is executed before its ADD counterpart. Also, as we can see, pride_step determines the “order” of decryption: when equal to 0, it simply corresponds to a sequential decryption (starting at index (IR ˆ pride_start)).
This ends the study of polymorphic techniques in METAPHOR. Both techniques we described mainly aim to impede any detection by emulation: however, in a sense, they also have a mutation role, not anymore in the form but in the behaviour. This proximity between signatures used for form analysis and signatures used for behaviour analysis is studied into more details in [Fil07].
METAPHOR’s metamorphic engine takes up 70% of the source code (11000 lines in all), the remaining 30% accounting for the infection routines (20%) and the decryptor’s creation routine (10%). This proportion isn’t uncommon: some metamorphic viruses devote up to 90% of their code to their metamorphic engine. The engine is used to mutate the virus body (more precisely the part to be encrypted) as well as the decryptor itself.
The engine works according to the following template, which The Mental Driller calls humorously accordion model:
One particularity of this engine, which conceptually differentiates it from its predecessors, is the use of an intermediate representation which allows to dissociate from the complexity of the underlying processor’s instruction set and to simplify the miscellaneous transformations and the code manipulation and creation. For instance, equivalences between x86 instructions are deferred until the reassembly stage, jumps at other code instructions are translated into a pointer perspective (that are much easier to manipulate, compared to offsets), etc.
1) Description of the pseudo-instruction set: METAPHOR uses a limited instruction set. It only considers instructions that are actually used by the code. Since this intermediate representation isn’t used when modifying the host code, this restriction is natural. This instruction set is organized as follows:
The opcode choices are motivated by the equivalent x86 opcode organization and by the sake of simplifying the manipulation of instructions and the coding of transformations. In particular, for the first type of opcodes, the opcode itself (for instance ADD) is encoded into bits 6..3, and the operand types into bits 2..0 and 7: bit 7 specifies whether the operands are 8 bits (for instance mov al, 12h) or 32 bits (for instance mov eax, 12h) whereas bits 2..0 specify the type of operands (Reg, Imm, etc.).
Finally, a pseudo-instruction is encoded in 16 bytes:
XX XX XX XX XX XX XX XX XX XX XX XX XX XX XX XX OP *--------- operands --------* LM *- instr -*
OP contains the instruction opcode, on one byte. Then the operands are encoded (register index, memory address or immediate value) on the following 10 bytes. Then LM (“Label Mark”) is a flag on 1 byte telling whether this instruction is the target of a branching instruction: when this is the case, the instruction can neither be deleted nor compressed with instructions preceding it. The last 4 bytes contain a pointer which has miscellaneous significations along the execution: during the disassembly, it contains the address of the initial x86 instruction, during the permutation, it contains the instruction’s address inside the non-permutated code, etc.
Once the virus decrypted its code, it gives control to it. After initialization of the variables and possible payload activation, it defines the form of next generation (internal organization of the code – where to put code, where to put data, etc.). Then it starts the code transformation process.
2) Disassembly: The x86 code is first disassembled into an intermediate representation which uses the previous instruction set. This procedure loads the intermediate code into the buffer pointed by variable InstructionTable. It also creates an array of labels which contains all instructions which are the target of a branching instruction. In the end, the computed intermediate code has been depermutated and the inaccessible code (dead code) removed: this is actually a direct consequence from the routine’s algorithm.
The x86 code is disassembled by following the execution flow. The algorithm uses an array, FutureLabelTable, which contains instructions which are waiting for their disassembly (namely these are the targets of conditional jumps and direct calls). Here is the algorithm:
Code permutation is carried out, as we will see, using unconditional jumps (no “opaque predicates” or similar tricks): during the disassembly, the JMP instruction used to join two permutated blocks is replaced by a NOP instruction and the disassembly continues with the new block. Given that the pseudo-code is built in a linear way, its final shape will be that of the depermutated code. Similarly, inaccessible code that was inserted will never be disassembled.
3) Compression: After disassembly and depermutation, the generated pseudocode is compressed. This cancels the expansion effects of the previous generations, since the compression rules are exactly the inverse of the expansion rules. There are five kinds of rules:
Notation !=Jcc denotes “any opcode that is not a conditional jump” and the notation !Jcc denotes the inverse of the last Jcc (for instance, JA and JBE). Furthermore, some of these rules might not be verified in the general case, but they are in the case of METAPHOR’s code.
The algorithm is simple. It compresses the code as much as possible. When it looks up the next instruction, it skips any NOP instruction that is not the target of jump or a call (flag LM is set). As long as it did not reach the end of the code, it tries to compress chunks of one, two or three instructions starting from the current instruction: if a compression occurs, it makes a three instructions step-back and continues. This allows to take into account any new reduction opportunity that might have appeared with an instruction created by the last reduction. For the sake of simplicity, instructions that are deleted are simply replaced by NOP instructions. In the end, the algorithm identifies all sequences of instructions that correspond to macro-instructions (APICALL_*, LINUX_SYSCALL*, LINUX_GETPARAMS, SET_WEIGHT) and replaces them accordingly. Also note that, for a reduction – of any type – to occur, no instruction, except the first one, shall be the target of a jump (flag LM).
The algorithm also allows to reduce sequences of operations into a unique operation. For instance, ADD Reg, X / SUB Reg, Y will be reduced into ADD Reg, (X - Y): these decompositions are created during the expansion. Finally, when a Jcc instruction is replaced by a JMP instruction, the following code is deleted (NOPed) until reaching a label (instruction with LM = 1).
Here is an example of compression (this code represents a basic decryption routine):
4) Variable reorganization: METAPHOR aims to mutate at the semantic level (instructions expansion / compression) and at the code level (permutation) as well as at the code behaviour level. We already mentionned previously that it was mutating the internal organization of the viral code. When the virus gains control, it allocates into memory a space of (340000h + X) bytes, where X is a random value between 0h and 01F000h. This space is then organized into 5 sections (see figure 5):
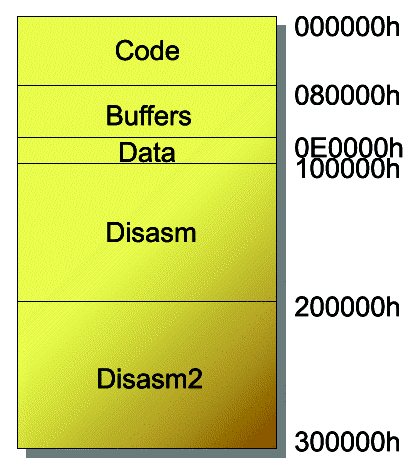
Fig. 5. METAPHOR’s memory organization (generation 0).
Before starting the mutation and replication process, sections are randomly permutated and each section is shifted by a random value between 0h and 7FFFh. In the end, the maximum required size (into memory) is: 300000h + 5 * 7FFFh = 340000h. Thus, upon execution, METAPHOR never has a unique memory access profile.
The virus contains about 200 global variables, each of these variables being allocated 8 bytes inside the Data section. These variables are accessed by their offset in that section. A register is specifically assigned, which isn’t modified during the virus execution, and which contains that section’s address. During generation 0, this base register is ebp. Thus, to access to the contents of variable InstructionTable, which is at offset 10h of the Data section, one uses:
Given that this register (ebp) is strictly reserved to data access, it is sufficient to spot all instructions that use it to identify read and write accesses to a variable and to list these very variables. Method IdentifyVariables does this job and replaces in each one of those instructions the offset by the index of the associated variable. Then the variables are shuffled: their organization inside the Data section is thus completely modified. Then, during reassembly, when an instruction uses one of these variables, the instruction is updated to contain the new base register (initially ebp) and the new offset of the referenced variable.
Thus the memory access profile is modified. This kind of transformation isn’t however taken to extremes. For instance, the code often reads the contents of pseudo-instructions, as in the following code excerpt (where esi and edi contain pseudo-instructions addresses):
This kind of access can be profiled, since the internal organization of an instruction does not mutate. However The Mental Driller could have taken memory access profile mutation to extremes by modifying this very internal organization of pseudo-instructions. Given the massive use of instructions accessing the contents of these pseudo-instructions, impact would have been even stronger, even though the mutation of the organization of pseudo-instructions is quite limited (might we add a few padding bytes to increase mutation possibilities).
Let’s note that, in this transformation’s implementation, variables are aligned on 8 bytes boundaries so that they can be randomly positionned on any one of the first 4 bytes: finally, only 4 bytes are used by a variable.
5) Permutation: Once the compression is over, the engine permutates the code by splitting it into blocks of random sizes, between F0h and 1E0h. When doing the splitting, the following breaks are avoided:
Once the code blocks have been computed and shuffled, the new code is built (and its address saved into variable PermutationResult). A jump at the first code block is inserted at the very beginning of the code and the code blocks are linked with each other using JMP instructions, except in the following cases:
The final result shall look like:
jmp @block1 @block4: ;-------------; ; block 4 ; ;-------------; (ends with a ret) @block2: ;-------------; ; block 2 ; ;-------------; @block3: ;-------------; ; block 3 ; ;-------------; jmp @block4 @block1: ;-------------; ; block 1 ; ;-------------; jmp @block2
6) Expansion: The expansion stage consists in applying the inverse rules from the compression stage. This method is called on the virus compressed pseudocode and, later, on the decryption routine’s code.
The first step consists in randomly modifying the used registers. A bijective transformation is applied, which takes into account the following requirements:
Then, the expansion can start: it will update registers as well as accesses to the virus’ global variables. The expansion’s result is stored in variable ExpansionResult. To control the size of expansion, a maximum level of recursivity is first chosen: it cannot be larger than 3. Then, for each instruction, we increment the recursivity level and we randomly transform it, by using the inverse compression rules. Intermediate instructions which are generated are also transformed. NOP instructions are ignored in the compressed code (to avoid an uncontrolled increase of size, after several generations).
When an instruction is generated, which uses a temporary memory address, this memory address points at the Data section and should not have been allocated for the virus global variables nor by any previous instruction in the current expansion chain. The VarMarksTable array is used to mark which addresses have been allocated. As for global variables, the allocated address is randomly aligned on one of the first 4 bytes. However, this is different in the case of the decryption routine since the memory has not been allocated yet (with a call to malloc): the space to be used by intermediate operations is then the data section that was allocated inside the host file for the decryption operations.
When an instruction uses an immediate value, this value is computationally decomposed into a sequence of operations that finally yield the expected immediate value. This expansion is managed by method Xp_MakeComposedOPImm. It uses operators ADD, AND, OR and XOR (the SUB operator is randomly generated when transforming ADD instructions). Here is for instance the algorithm used to generate a MOV Dest, Imm instruction:
choose randomly among:
In addition, dead code is inserted, with probability 1/16, after each expansion of an instruction of the compressed code (if this instruction’s opcode was a CMP, TEST, CALL or APICALL_STORE, a mere NOP is inserted):
7) Reassembly: The last stage consists in assembling the pseudo-code into valid x86 code. When several translations are possible, the algorithm chooses one at random. Also, short jumps and long jumps are randomly used (when a short jump is possible), and jumps at subsequent addresses are stored in array JmpRelocationTable, in order to be updated in the end. After completion of this stage, the code is ready for encryption and copy out in the host.
1) Pseudo-Random Numbers Generator (PRNG): METAPHOR makes a heavy use of random numbers. It uses its own pseudo-random numbers generator, with two seeds, seed1 and seed2, which are initialized depending on the UNIX date for seed1 and on the code’s first bytes for seed2. Then a random value is generated using the following algorithm (ror_X denotes right rotation by X bits):
Though this may not be obvious at first sight, the second seed is very weak, given furthermore that it is initialized depending on the code’s first bytes which have a low randomness: thus we get, in the worst case, a cyclic generator of 32 pseudo-random numbers (as soon as seed2 reaches value 0x00000000 or value 0xFFFFFFFF). For a random seed2, a few tests allow to compute the PRNG’s period about 40000, which is barely better that the glibc’s generator (random () function), whose statistical properties are particularly weak and whose period is in the order of 30000.
Polymorphic viruses usually have their own pseudo-random generator, often of poor quality, which protects them at least from a heuristic alert due to a strong utilization of a system’s PRNG. Yet, some generators exist that are quite powerful and have a small cost, but their use in polymorphic viruses is scarce. Here are some of them:
2) “Genetic” techniques: METAPHOR combines genetic characteristics to its generator. Here is the principle. The virus contains some sort of genetic material which will have a tendency to favour some behaviours rather than others. On each replication, this genetic material is updated with a small random variation from the preceding material.
For instance, a gene contains the current propension of the virus to encrypt its code or not: the virus initially encrypts its code with probability 1/16. Depending on its decision, the gene will be altered in favour or in disfavour of encryption: if the virus encrypts its body, it will have next time a higher probability to encrypt again its body, and conversely. Thus after a few generations, either the code will have a strong propension to encryption, or a strong propension to absence of encryption. The propension strengh is related to the survival time (and to the number of replications) of the virus. Thus, if the virus has a strong propension to encryption, this means that most of the previous generations chose encryption and survived: this is kind of an implementation of natural selection, where viruses are preys and antiviruses are predators. Thus, let’s imagine that the antivirus easily detects encrypted replications of the virus (using statistical entropy analysis for instance) but not unencrypted replications. In this case, encrypted replications will be detected before being able to replicate and increase their propension to encryption, and in the end, most of the survivors will come from unencrypted ancestors, with a high propension to no encryption.
METAPHOR contains a genetic material of 24 genes. In other words, 24 of its choices depend on its genetic history and its survival abilities. These genes are used for instance for:
Given that the virus does not store any information in its host other than its code, it must still be able to update its genetic material, from one generation to another. This is where SET_WEIGHT macro-instructions come into play: they’re located on disassembly and, on reassembly, the “evolved” gene is used.
Here is the algorithm used to update the genes (function CheckForBooleanWeight). We notice that the genes values cannot exceed a minimal and a maximal threshold (thus the associated probability never reaches 1 or 0).
For a more detailled analysis of genetic viruses, one may refer to M. Ludwig’s books [Lud95], [Lud93].
Analysis of METAPHOR comes to an end. As we saw, several advanced techniques of polymorphism and of anti-emulation / anti-heuristic protection are implemented in this virus. Nevertheless they’re not taken to their extremes and thus this mutation model is still detectable, mainly because of the following “weaknesses”:
É. Filiol studies into more details some aspects of METAPHOR in [Fil07], from a theoretical point of view, and most notably regarding the detection barrier on which METAPHOR sits astride: if it mostly inclines towards detectability, some modifications would be sufficient to have it incline towards the other side (see the POC virus PBMOT). To sum up, METAPHOR is a highly advanced virus, which could be really dangerous with a few improvements (PBMOT certainly is the most appropriate proof). Other advances, as on the field of functional polymorphism, would also give metamorphic viruses more sophisticated means of defence against detection.
If polymorphic and above all metamorphic techniques described in this document enable viruses to protect themselves in a more efficient way against detection, their sophistication mostly stems from antiviral protection. For antiviral protection is in fact eternally submitted to two paradoxes:
Also, it should be noted that the state of the art of current metamorphic techniques (with viral protection purpose) is not representative of the threat they represent. Some antiviral experts sweep blatantly away – recently again [She07] – this threat on the pretext that it never actually proved itself except for proving its own uselessness. And as a matter of fact, the history of metamorphic viruses tends to corroborate this: there are few of them, most of which are poorly accomplished and contain critical flaws (bugs or conception flaws which make detection easy). In the same time, development of rootkit techniques draws away attention. Yet, both threats are real, with different maturities, but none of them should be overlooked. Even though the second one is mostly implemented in worms, which currently represent the most important infectious threat, and even though it is more technical than the first one, and thus within the means of more hackers.
All in all, if virus writers were a bit less “in a hurry” and refined their techniques, the antiviral community could be quickly overtaken. An advanced use of syntactic and functional polymorphism techniques, combined with advanced stealth techniques, would theoretically make the complexity of the detection problem prohibitive or even undecidable [Fil07] (POC virus PBMOT).
Philippe Beaucamps is a PhD student at the CNRS / LORIA in Nancy, France. He works on the modelization of viral infections, and on formal and practical malware detection and protection.
Contact address: Loria, Équipe Carte, 615 rue du Jardin botanique, CS 20101, 54603 Villers-ls-Nancy Cedex France
1 MUTATION ENGINE (MTE) by Dark Avenger, TRIDENT POLYMORPHIC ENGINE (TPE), NUKE ENCRYPTION DEVICE (NED) and DARK ANGEL’S MULTIPLE ENCRYPTOR (DAME).
2 VIRUS CONSTRUCTION LAB (VCL), PHALCON/SKISM MASS-PRODU-CED CODE GENERATOR (PS-MPC) and PHALCON/SKISM’S G2 VIRUS GENERATOR (G2).
3 i.e. targetting .NET assemblies.
4 METAPHOR is also known as SIMILE or ETAP.
[Back to index] [Comments (0)]