William Arnold, Gerald Tesauro
Virus Bulletin conference
September 2000
 Download PDF (82.49Kb) (You need to be registered on forum)
Download PDF (82.49Kb) (You need to be registered on forum)Heuristic classifiers which distinguish between uninfected and infected members of some class of program objects have usually been constructed by hand. We automatically construct multiple neural network classifiers which can detect unknown Win32 viruses, following a technique described in previous work (Kephart et al, 1995) on boot virus heuristics.
These individual classifiers have a false positive rate too high for real-world deployment. We find that, by combining the individual classifier outputs using a voting procedure, the risk of false positives is reduced to an arbitrarily low level, with only a slight increase in the false negative rate. Regular heuristics retraining on updated sets of exemplars (both infected and uninfected) is practical if the false positive rate is low enough.
Stateless heuristic classifiers have augmented virus scanners with the ability to detect new viuses since the early days of virus scanners.1 (This is as opposed to classifiers that use a history of object states or state changes, such as heuristics that use a checksum database, or heuristics that use audit trail data.) These classifiers have been constructed for individual classes of viruses, largely by hand, with various ad-hoc designs. Some have been very successful at detecting new, unknown viruses. A few (see endnote 5) have nearly achieved their goals of low false negatives and zero false positives.
Linear classifiers with a threshold are one of the simpler designs for a heuristic virus detector (see Figure 1.) Linear classifiers are well understood, generalize well to new inputs, and training procedures for automatic adjustment of weights are well documented. Human experts have usually performed selection of the features used as classifier inputs. Kephart et al 2/3/8 describe a technique for automatically selecting simple static features indicative of the presence of viruses, namely small sequences of bytes called n-grams. We loosely followed this procedure in our work. As in previous work, we found that multi-layer networks overfitted the data even if we used a very small number of hidden units. Overfitting happens when the classifier learns the training set too well. The resulting classifier performs poorly on data not used for training.
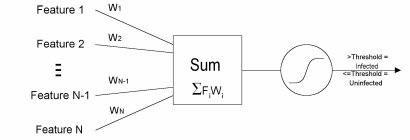
Figure 1: Single layer neural classifier with threshold
False positives have been one major problem with heuristic virus detectors. Anti-virus vendors must make a tradeoff between false positives and false negatives. As the sensitivity of the detector to viruses is increased, the false positive rate generally increases as well. Scanner designers often resort to a hybrid design, with an over-sensitive detector susceptible to false positives, and a method of suppressing known false positives. Such a design is a trap, because after the suppression table starts to become filled with entries for false positives encountered in the field, the scanner engineers become reluctant to make changes to the heuristics engine for fear that their customers will encounter an entirely new set of false positives.
We attempted to solve the false positive problem by constructing multiple networks using distinct, unshared features, and then using a voting procedure, so that more than one network would have to agree on a positive. This worked remarkably well at eliminating false positives on our test-set. On reflection, it appears that most false positives issued by file classifiers that use small n-grams as features are due to the random presence of an n-gram feature in a file.
Classifier training procedures alone cannot learn to avoid random false positives of this type. With a voting procedure and a voting threshold greater than 1, more than one component network needs to agree on a false positive for the final output to be a false positive. It is very unlikely that there will be more than one random false positive on a file.
The procedure we used requires a large collection of uninfected Win32 executable files. By construction, most uninfected files do not contain any viral features, and we need a reasonable number of files that do contain viral features on which to train. Unlike endnote 2, we have no reasonable way to augment our set of uninfected files artificially. To reduce the amount of effectively random data in the collection, all the install programs that we could find with large compressed data regions were removed except for one copy of each particular installer. We eliminate most compressed data because they appear to be random when digested into n-gram statistics, and pollute the n-gram statistics (for small n-grams) with a `floor' of non-zero counts. For example, if bigram statistics are gathered over 1 GB of random data, the expected count for any bigram would be around 16 KB. Our uninfected corpus of 53,902 files was evenly divided into a training set and a test-set.
Our procedure also requires a collection of infected files, with multiple replicants per virus. The collection of 72 replicant sets was also evenly divided into a training set and a test-set. Normal automated analysis tools are used to determine empirically regions of each virus constant across all instances of the virus. We used these regions as the input data for selection of feature candidates. They could include decrypted regions of viruses run under emulation, if the detector would be used in a virus scanner capable of running Win32 executables under emulation. For our experiments we chose unencrypted viruses and used only regions of the viruses that are scanned. We conservatively decided to use the entire clean file, rather than just the parts examined by a virus scanner. This is similar in spirit to the artificial uninfected object set augmentation described in endnotes 2 and 3, except that we are using real programs. Another potential problem with using just the parts of files examined by a virus scanner is that it constrains the development process; changes to the scanning engine could affect the false positive rate in the heuristic engine.
For our experiments we chose 3 and 4 as our n-gram lengths. The later parts of the detector generation procedure could easily be adapted to use features other than n-grams, or features more complex than n-grams. Other feature sets could be generated by a human expert (e.g. the set described by Ször6), or by automated analysis. We have not explored other sorts of automated feature discovery. Obvious things to try include automated feature extraction from emulator traces, and automated feature extraction from behavior logs/audit trails. There are far too many 3-grams and 4-grams in the constant regions of currently known Win32 viruses to use them all as features. Fortunately, most of them are extremely poor at discriminating between infected and uninfected files, so we pruned out most of them from the feature set. We use a simple threshold-pruning algorithm. From the constant parts of each virus, we select the n-grams which appear in our corpus of uninfected files fewer times than a threshold T. For our experiments, we chose threshold values less than the values which would be expected if the uninfected corpus were composed entirely of random data. The uninfected corpus is not composed of random data, so some n-grams appear less frequently than they would in random data.
Viruses that have no candidate n-grams are removed from the training set in the next steps. For n-grams which do not appear in the corpus of uninfected files, we use an estimated count based on the frequency of the components of the n-gram, as described.4 If a very small pruning threshold is chosen, use of estimated counts is especially important to usefully rank n-grams. We do not select features indicative of the absence of viruses. This potential enhancement of the method remains to be explored. Dmitry Gryaznov5 described heuristics with such negative features and claimed very good results, so we are hopeful that inclusion of negative features will be useful. The cover generation parts of the method would need to be altered to allow for negative features. See Table 3 for results of tests in which we adjusted the feature-pruning threshold. We conclude that the feature pruning should be as aggressive as feasible. The quality of classifiers depends a great deal on the quality of the features used to build them.
We use a greedy algorithm to generate C-independent, complete n-gram 1-covers of the virus training set. A complete 1-cover consists of a set of features (n-grams) selected such that at least one feature is present in each virus. The algorithm is `greedy' because at each selection step, the algorithm selects the unused feature that covers the most remaining uncovered viruses. We generated 8 covers for our experiments. N-grams are not reused, so a limited number of covers can be generated. Eliminating reuse of n-gram features increases the probability that the individual networks will be independent. Our method does not work if there is a high degree of correlation between classification errors by the voted networks.
We did not attempt to generate optimal covers. The greedy algorithm has the property that it preferentially selects features that cover as many viruses as possible. This is a key feature of the method; we want the method to select `strong' features that are found in many different viruses. Optimal (or near optimal) covers will be tried in future work. Optimal covers may make more efficient use of the usable n-gram feature data, and allow more covers to be generated from the same quantity of data.
We tried using incomplete covers as well. In an incomplete cover, the features do not cover all viruses. For example, if we only use features that cover two or more viruses, the feature set might not cover some viruses. Nets based on incomplete covers had a higher false negative rate on the test set than covers based on complete covers. This may be due to the fact that many viruses are trivial variations on other viruses, and so coincidentally share randomly chosen byte sequences with their variants. Nets based on incomplete covers appear to have lower false positive rates in our tests. They have fewer n-gram features and hence should have fewer random false positives.
We constructed input vector sets for each of the 8 covers. Each vector consists of values for each feature for a particular exemplar (values consist of counts for each n-gram feature in the virus sample or clean sample) and the correct output value (0 or 1 for our networks). Input sets are constructed for both the test and training set. A fictitious example of an input vector for a virus is
2.000 0.000 1.000 0.000 0.000 0.000 1.000 0.000 0.000 1
We used linear networks. The number of viruses used in our experiments was too small to support multi-layer networks, according to the usual rules of thumb. We tried multi-layer networks anyway, and as expected saw overfitting even with a small number of hidden units. We expect that multi-layer networks will perform better as more Win32 viruses appear. (For 32 features and 4 hidden units, the number of exemplars should be significantly larger than O(32*4).) Typical back-propagation training software (see endnote11) was used to train the linear networks. We save the computed outputs for each trained network for every vector in its test and training sets. The outputs are squashed through a sigmoid output unit, as shown in Figure 1, and take on continuous values between 0.0 and 1.0 inclusive:
sigmoid(x) = 1.0/(1.0+exp(-x));
The network training software we use tries to minimize error over the training set, but this is not the same as minimizing discrete classification error counts. We sweep through a range of possible output thresholds (between 0 and 1) to find a threshold which minimizes total classification errors across all the individual networks and all the training inputs, giving equal weight to infected and uninfected errors.
For a particular input vector, if the output O is less than threshold OT, then the discrete output is 0 (uninfected), else the discrete output is 1 (infected). We tried using different thresholds for each linear network but settled on a single threshold for all the linear networks. The single threshold value used in the initial experiments described below was set to 0.65 for 4-gram inputs and 0.5 for 3-gram inputs. In subsequent experiments with the training and test sets swapped, the corresponding values were 0.575 for 4-grams and 0.4 for 3-grams.
The use of an output threshold or sigmoid (we use both) means that combinations of individual linear networks are not linear (i.e. can compute non-linear functions of the input). Combinations of completely linear networks are equivalent to a single larger linear network. We have found that a single large linear network does not perform as well as a non-linear combination of smaller networks (see Table 3).
We use voting to combine the outputs from each network into a single result. For a voting threshold V and networks N1,...N8, if N1+N2+...N8 > V, then output value is 1 (infected), else output value is 0 (uninfected) (see figure 2). The voting threshold is selected by sweeping across the possible vote threshold values (1 to 8) and selecting a threshold with zero false positives and minimum false negatives on the training set.
We conservatively increment the threshold by one to further minimize false positives due to an n-gram appearing in a clean file by chance. Effectively we are forming a type of multi-layer perceptron (MLP)11 that is easily tuned to minimize specific types of misclassifications.
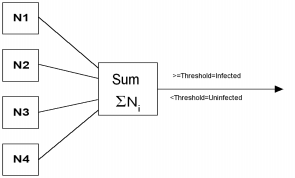
Figure 2: Combining individual networks with voting. Each individual network outputs a 1 or 0.
See Table 1 and Table 2 for the voting results for some of our tests. The results for 4-gram features are convincing; the voting appears to be able to eliminate false positives with a moderate effect on the false negative rate. 3-gram features appear to be too short to classify Win32 viruses; the false negative rate is too high at a voting threshold sufficient to eliminate false positives.
While not rigorous, it may be useful to combine the test-set and training set and rebuild the networks, using thresholds similar to those empirically determined in the previous steps with a split training and test set. The hope is that the combined sets will result in a classifier more powerful than one built on half the full set of uninfected and infected files, but with similar false-positive characteristics.
A more rigorous way of attacking this problem would be to use multiple random 90/10 partitions of the infected/uninfected data rather than a single 50/50 partition. Thresholds could be selected over each 90/10 partition and the thresholds averaged. We have not yet attempted this later approach.
Results so far indicate that detectors generated by this procedure are not sufficient to serve as the sole Win32 virus detection heuristics in a scanner. They do appear to be good enough to be very useful as an augmentation of expert-designed heuristics, and they would serve as sole heuristics were nothing else available. Similarly, expert-designed heuristic features would very likely be useful as additional features in an otherwise automatically generated network. False positives can occur for several reasons. The method described in this paper provides a way of greatly reducing false positives caused by random appearance of features in uninfected files. Uninfected files may legitimately contain some characteristics similar to those in viruses.
| 1 of 8 | 2 of 8 | 3 of 8 | 4 of 8 | 5 of 8 | 6 of 8 | 7 of 8 | 8 of 8 | Single Large Network | |
|---|---|---|---|---|---|---|---|---|---|
| TrnFPos | 12; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 |
| TrnFNeg | 0; 7 | 0; 0 | 1; 0 | 1; 1 | 3; 6 | 8; 8 | 11;11 | 17;14 | 0; 0 |
| TstFPos | 50;29 | 0; 3 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 |
| TstFNeg | 3; 0 | 3; 4 | 10;13 | 15;15 | 16;17 | 18;19 | 20;21 | 22;23 | 14;15 |
Table 1: Effect of voting threshold on false positives and negatives for 8 single-layer networks using 4-gram features. The networks use complete covers. Training and test sets each contain 36 infected and approximately 27,000 uninfected exemplars. The values are misclassification counts for training false positives, training false negatives, test false positives, and test false negatives. Results after semicolon are after swapping test-set and training set. Note a sign of overfitting with the large network; there is a large difference between the training false negative count(0) and the test false negative count (14).
| 1 of 8 | 2 of 8 | 3 of 8 | 4 of 8 | 5 of 8 | 6 of 8 | 7 of 8 | 8 of 8 | Single Large Network | |
|---|---|---|---|---|---|---|---|---|---|
| TrnFPos | 5; 6 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0;0 |
| TrnFNeg | 14;13 | 22;18 | 25;22 | 32;29 | 32;34 | 36;36 | 36;36 | 36;36 | 19;18 |
| TstFPos | 24;24 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 7;4 |
| TstFNeg | 15;17 | 23;22 | 26;26 | 36;30 | 36;31 | 36;36 | 36;36 | 36;36 | 22;23 |
Table 2: Effect of voting threshold on false positives and negatives for 8 single-layer networks using 3-gram features. The values are misclassification counts for training false positives, training false negatives, test false positives, and test false negatives. The exemplar sets were heavily dominated by uninfected exemplars. The networks use complete covers. Results after semicolon are after swapping test-set and training set. The single large network did not achieve zero false positives on the test-set.
Our experience with a similar, simpler boot virus classifier was that certain uninfected boot sectors were functionally similar enough to viruses to cause a false positive.2 We do not have enough experience with the voting method to know whether it will suffer from similar problems in the field.
Heuristics based on behavioural features found during dynamic program analysis (e.g. emulation) would be more resistant to this type of false positive, as would heuristics based on features found during audit trail analysis. Related research into the automated discovery of features in audit trails has had limited successes so far. See endnote 10 for an example of the state of the art in audit trail analysis.
Sometimes files in the field contain fragments of viruses. This may be due to an incomplete repair, or to incomplete virus infection, or to the vagaries of the file system on a machine that once was infected, or due to a naïve implementation of a virus detector which contains unencrypted fragments of virus, or for other reasons. Static heuristics are vulnerable to false positives on these types of files. To a great extent, the virus-scanning engine (into which heuristics are fitted) can limit some of these types of false positives by scanning only active regions of files.
In some situations, lower thresholds and hence lower false negative rates and higher false positive rates might be acceptable. For example, anti-virus vendors receive a steady stream of samples from customers. Only a fraction of these samples are infected by viruses known to virus scanners. Heuristics with high false positive rates might be acceptable as an aid in sorting the remainder of these queues. In general a high false positive rate is more acceptable when real positives (undetectable by other inexpensive means) are more common. A high false positive rate may also be acceptable if it does adversely not affect users.
The technique described can be used for other types of viruses, so long as we have an adequate collection of uninfected files and different viruses to train on. The general rule of thumb in classification is that the number of adjustable parameters in a classifier (weights, in a neural network) should be substantially less than the number of training exemplars. For a linear network, the adjustable parameters are the weights associated with each feature. With a small feature set of 16-32 features, automated training will work, without overfitting, if there are a larger number of viruses and clean files which contain the features. Multi-layer networks would require substantially more viruses. For a network with 1 hidden layer, the number of parameters is approximately number of features times number of hidden units. For a small network with 32 features and 4 hidden units, the number of viruses would need to be roughly 128 or larger.
In the immediate future, we plan to do more runs with random test and training set partitions, to validate our method of selecting the voting threshold. We need to incorporate the resulting networks into a real virus scanner. There are several directions near future research could take. We are interested in training on more viruses, and on training multiple layer networks. We have not yet tried combining networks based on multiple covers; e.g. voting on the outputs of 4 networks based on 2-covers. Optimal covers might make better use of the available training data. An interesting exploratory direction of research is automated discovery of virus features other than n-grams. Examples include discovery of features in virus scanner emulator traces, in real-time scanner audit trails, and in system audit trails.
Feature pruning is a critical part of this procedure. We performed several tests with adjustments of the feature-pruning threshold. Results are summarized in Table 3. They suggest that further work on feature selection and pruning would be useful. For a linear network, the features should by themselves have reasonable discrimination power between infected and uninfected exemplars. They should also be frequently found amongst one class or the other. For multi-layer networks, these constraints might need to be relaxed; a multi-layer network can use weak features if strong features can be constructed from combinations of the weak features.
| T = 2 | T = 4 | T = 8 | T = 16 | |
|---|---|---|---|---|
| TrnFPos | 0 | 0 | 0 | 0 |
| TrnFNeg | 1 | 13 | 13 | 23 |
| TstFPos | 0 | 0 | 0 | 0 |
| TstFNeg | 10 | 15 | 16 | 20 |
Table 3: Effect of feature pruning threshold T on performance of resulting classifiers, each consisting of 8 voted single-layer networks using 4-gram features. Any viral 4-grams appearing more than T times in the uninfected training data are removed from the list of candidate features. The values are misclassification counts for training false positives, training false negatives, test false positives, and test false negatives. From this we conclude that aggressive feature pruning is important, and that highly discriminating features are essential for a linear network.
In Table 4, we show an example of threshold selection for a single large linear network. The network is really too large for our training set, and overtraining appears to result. The results for the swapped test and training set are substantially different than the results for the unswapped sets, which is not confidence inspiring. It would be interesting to try tests with multiple random partitions of the test and training set.
| T=0.1 | T=0.2 | T=0.3 | T=0.4 | T=0.5 | T=0.6 | T=0.7 | T=0.8 | T=0.9 | |
|---|---|---|---|---|---|---|---|---|---|
| TrnFPos | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 |
| TrnFNeg | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 | 0; 0 |
| TstFPos | 12; 2 | 7; 0 | 3; 0 | 2; 0 | 2; 0 | 2; 0 | 0; 0 | 0; 0 | 0; 0 |
| TstFNeg | 12;13 | 12;14 | 13;15 | 14; 16 | 14;16 | 14;16 | 14;16 | 14;17 | 14;17 |
Table 4: Adjusting the threshold of a single large linear network, based on 8 complete 4-gram covers. The values are misclassification counts for training false positives, training false negatives, test false positives, and test false negatives. Results after the semicolon are after swapping test set and training set. Note a sign of overfitting; there is a large difference between the training false negative rate and the test false negative rate.