Alun Lloyd, Robert May
Science, New Series, Vol. 292, No. 5520. (May 18, 2001), pp. 1316-1317.
ISSN 0036-8075
May 2001
 Download PDF (451.72Kb) (You need to be registered on forum)
Download PDF (451.72Kb) (You need to be registered on forum)A. L. Lloyd is in the Program in Theoretical Biology, institute for Advanced Study, Einstein Drive, princeton, NJ 08540. USA. E-mail: alun@alunlloyd.com R. M. May is in the Department of Zoology, University of Oxford, South Parks Road, Oxford OX1 3PS. UK. E-mail: robert.may@zoo.ox.ac.uk
The Internet and the world wide web (WWW) play an ever greater part in our lives. Only relatively recently, however, have researchers begun to study how the patterns of connectivity in these networks affect the spread of computer viruses within them (1, 2) and their ability to handle perturbation or attack (3). Many models for communication can be formulated in terms of networks, in which nodes represent individuals (such as computers, web pages, people, or species) and edges represent possible contacts between individuals (network links, hyperlinks, social or sexual contact, and species interactions). The study of communication networks therefore has interesting parallels both with conventional epidemiology (4, 5) and with the ability of ecosystems to handle disturbances.
In a recent paper in Physical Review Letters, Pastor-Satorras and Vespignani (6) explore a dynamical model for the spread of viruses in networks of the kind found in the Internet and WWW (7, 8). In striking contrast with the usual models for the spread of infection in human and other populations, they find no threshold for epidemic spread: Within the observed topology of the internet and WWW, viruses can spread even when infection probabilities are vanishingly small. They also find that, in its early phase, the epidemic spreads relatively slowly and nonexponentially, again in contrast with the initial exponential behavior in conventional epidemics. These are notable findings, and the authors suggest they may be relevant to other types of social networks.
The importance of spatial structure for disease transmission has long been recognized (9).Locally structured networks often have many intermediates in paths between any given pair of individuals. They can also exhibit clique behavior, with pairs of connected individuals sharing many common neighbors, reducing the opportunities for secondary infection events. As a result, diseases may spread more slowly when contact is mainly local, compared with well-mixed situations. Conversely, earlier studies showed that even infrequent long-distance infection events can enhance disease spread (9). This foreshadowed some aspects of recent work on "small world" networks (10) and on the recent spread of foot and mouth disease in the UK (11).
In contrast to such results, which derive from the spatial structure of networks, Pastor-Satorras and Vespignani's results largely derive from the scale-freecharacter of the internet and WWW (6). Scale-free networks (see the figure) can arise when a network grows through new nodes being linked preferentially to the most highly connected existing nodes (12). The probability for a node to be connected to k other nodes obeys a power law distribution, 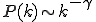 . In the case of the Internet and WWW, the observed exponent
. In the case of the Internet and WWW, the observed exponent 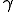 lies between 2 and 3 (7,8).
lies between 2 and 3 (7,8).
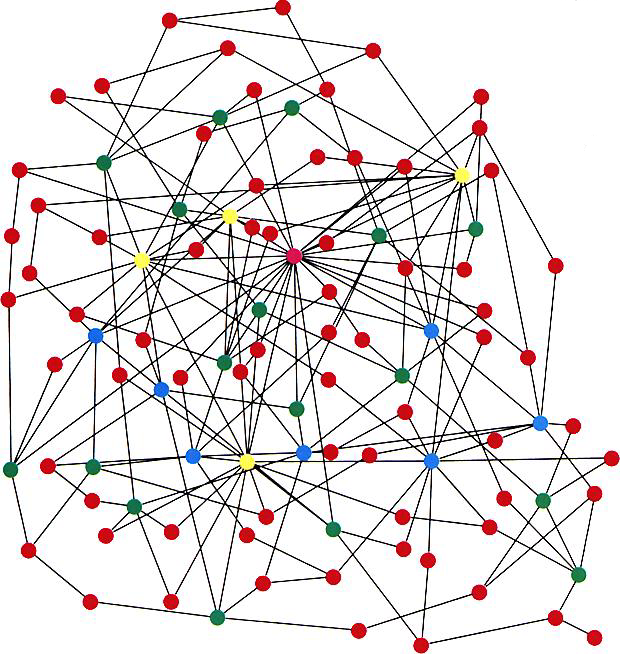
No matter of scale. Example of a scale-free network, consisting of 100 nodes, generated with the algorithm of Barabási and Albert (12). In order of increasing connectivity, the nodes are colored red, green, blue, and yellow, with the most highly connected nodes colored magenta. Note the small number of highly connected nodes; the majority of nodes have few connections.
Pastor-Satorras and Vespignani simulate the spread of computer viruses with a "susceptible-infected-susceptible" (SIS) model, in which susceptible individuals acquire infection at a rate 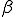 upon contact with an infected node and subsequently recover from the infected to the susceptible state after an average time D. In their scale-fice network,
upon contact with an infected node and subsequently recover from the infected to the susceptible state after an average time D. In their scale-fice network, 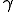 equals 3 (12) and the least connected nodes have m connections. The average connectivity,
equals 3 (12) and the least connected nodes have m connections. The average connectivity, 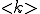 , is then 2m. The authors show th[Cat the results obtained with this model agree with observed patterns of viral spread and persistence. The system eventually settles to a steady state, in which the fraction of infected nodes is
, is then 2m. The authors show th[Cat the results obtained with this model agree with observed patterns of viral spread and persistence. The system eventually settles to a steady state, in which the fraction of infected nodes is 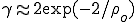 , where
, where 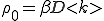 . Epidemiologists would call
. Epidemiologists would call 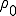 the "basic reproductive number" for the disease - the average number of infections produced by an infected individual in a wholly susceptible population - assuming a homogeneous network (that is, all nodes are assumed to interact with the same number of other nodes, namely the average, 2m).
the "basic reproductive number" for the disease - the average number of infections produced by an infected individual in a wholly susceptible population - assuming a homogeneous network (that is, all nodes are assumed to interact with the same number of other nodes, namely the average, 2m).
However, spurred largely by the need to understand the spread of human immunodeficiency virus (HIV) within complex networks of sexual partnerships, traditional epidemiology has advanced well beyond homogeneous models. The basic reproductive number, 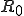 , for HIV and other infections spread by binary contacts within complex networks, including those studied in (6), is
, for HIV and other infections spread by binary contacts within complex networks, including those studied in (6), is ![R_0=\rho_0[1 + (CV)^2]](../img/cache/0fa24b2a131bf79c97fb9513f264d70b.gif) (5, 13, 14), where CV denotes the coefficient of variation (the standard deviation divided by the mean) of the node-connectivity distribution. This expression shows that heterogeneity within the network leads to an increase in the basic reproductive number. The reason for the absence of a threshold for the spread of infection in Pastor-Satorras and Vespignani's study is now clear: Their scale-free distribution has infinite variance, and hence
(5, 13, 14), where CV denotes the coefficient of variation (the standard deviation divided by the mean) of the node-connectivity distribution. This expression shows that heterogeneity within the network leads to an increase in the basic reproductive number. The reason for the absence of a threshold for the spread of infection in Pastor-Satorras and Vespignani's study is now clear: Their scale-free distribution has infinite variance, and hence 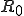 always exceeds unity, no matter how small the homogeneously approximated quantity
always exceeds unity, no matter how small the homogeneously approximated quantity 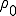 may be.
may be.
The nonexponential nature of the initial spread of infection has also been noted in heterogeneous epidemiological models for HIV (13). The initial exponential epidemic phase is rapidly curtailed because the highly active classes quickly saturate with infection, giving way to a more gradual increase, with new infections largely coming from the slower dissemination of infection to less active classes.
In SIS models, the fraction infected at any one time comes almost entirely from continual reinfection of the most highly connected nodes. In reality, these are exactly the sophisticated nodes most likely to avoid this fate. Moreover, for many computer viruses, infected nodes are likely to recover to an immune, rather than a susceptible, state (by using antiviral software or simply losing susceptibility to "I LOVE YOU" enticements). In this case, the somewhat more complicatedclass of "susceptible-infected-recovered" (SIR) epidemiological models is more appropriate.
In SIS situations,we can observe endemic levels of infection in a closed population, whereas in SIR models, the epidemic waxes and then wanes as the progressing epidemic reduces the number of susceptible nodes. Again, analytic and simulation-based results on the spread of sexually transmitted diseases within heterogeneously connected networks are informative here. For instance, Anderson and May (5, 13) have derived formulas for the fraction of the population, I, ever infected in an SIR epidemic. Interestingly, for Pastor-Satorras and Vespignani's scale-free distribution, this proportion is of much the same form as the asymptotic fraction infected in the SIS model: 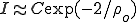 (a detailed calculation shows that the constant
(a detailed calculation shows that the constant 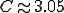 ). Note that in those circumstances where
). Note that in those circumstances where 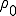 is small, so that
is small, so that 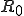 exceeds unity by virtue of the infiite variance in the contact distribution, the fraction infected (both in the steady state for SIS and in total as the epidemic sweeps through for SIR) will be very small.
exceeds unity by virtue of the infiite variance in the contact distribution, the fraction infected (both in the steady state for SIS and in total as the epidemic sweeps through for SIR) will be very small.
At first sight, it might seem as if the extreme heterogeneity exhibited by the scale-free networks of Pastor-Satorras and Vespignani makes them poor models for human interactions. Complicated networks of social interactions cannot be treated as if they were homogeneous (5, 14), but heterogeneity is often low in networks describing friendships between individuals (15), which might be appropriate models for diseases passed by casual social contact (or computer viruses that use e-mail address lists foundon infected machines). Pastor-Satorras and Vespignani's results may be less appropriate for diseases passed by social contact.
On the other hand, sexual partnership networks are often extremely heterogeneous because a few individuals (such as prostitutes) have very high numbers of parhers. Pastor-Satorras and Vespignani's results may be of relevance in this context. The study highlights the potential importance of studies on communication and other networks, especially those with scale-free and small world properties, for those seeking to manage epidemics within human and other animal populations.