Ferenc Leitold
In U. E. Gattiker (Ed.), Conference Proceedings EICAR International Conference, pp. 24-30
ISBN 87-987271-2-5
June 2001
 Download PDF (57.24Kb) (You need to be registered on forum)
Download PDF (57.24Kb) (You need to be registered on forum)Ferenc Leitold has graduated at Technical University of Budapest in 1991. He received his Ph.D. at Technical University of Budapest too, in 1997 in the theme of computer viruses. Currently he teaches in the Department of Information Systems at Veszprém University. He teaches computer programming, computer security and computer networks. His research interest is based on computer viruses: mathematical modeling of computer viruses, automatic methods for analysing computer viruses and testing anti-virus software.
Mailing Address: Ph.D. Ferenc Leitold, Kupa str. 14. H-8200 Veszprem, HUNGARYDescriptors computer virus, polymorphic virus, virus detection problem, Turing-machine, Random Access Stored Program Machine, RASPM with ABS
Theoretically it is impossible to generate a program which can solve the general virus detection problem. This theorem has been proved in different ways in the literature. Since the general virus detection problem is not solvable, we have to reduce the problem: we can deal "only" with a subset of viruses. For example, we can limit the storage space of viruses or we can limit the execution time of viruses. Theoretically in these cases it can be proved that there is an algorithm for the virus detection problem. On the other hand, we can reduce the general virus detection problem if we deal with the known viruses only. In this paper, I would like to examine the virus detection problem, the possible reductions of the virus detection problem and, of course, I would like to highlight the usability of the virus detection algorithms in the practice too.
There are some well-known computation models for the analysis of single algorithms, such as Random Access Machine, Random Access Stored Program Machine, the Turing-machine, etc. (Aho, Hopcroft, Ullman, 1975; Davis, 1958; Lewis, Papadimitriou, 1981; Salomaa, 1985; Hopcroft, Ullman, 1979; Regan, 1993; Bshouty, 1993). There are very useful definitions for the cost criterion on these models, but they cannot be used for the analysis of program codes interacting with other programs, for example, of the computer viruses (Leitold, Csótai, 1992; Virus Bulletin, 1993). Keeping the cost criterion, a new model, Random Access Stored Program Machine with Attached Background Storage has been developed. (Leitold, 2000) In the first part of this paper, the general virus detection problem is reviewed. After examining the general virus detection problem, the possible reductions of the problem are discussed: limiting the space used by viruses and limiting the execution time of viruses. In the last part of this paper the virus detection methods used in the practice are discussed.
With the emergence of viruses, the problem of virus detection also emerges.
Definition: The virus detection problem is a question of theory of algorithms, namely whether a specific algorithm exists or not which is able to decide that a specified program area contains a virus able to be spread or not.
Here we assume that all information is available concerning the format of the program area. It means that in the case of an executable file the instruction set of the processor and the operation of each command is known; in the case of source files the syntax of the programming language and the operation of the compiler is fully known.
Considering the Church-theorem (Aho, Hopcroft, Ullman, 1975; Lewis, Papadimitriou, 1981; Salomaa, 1985), if there is an algorithm which is able to solve the virus detection problem, then a Turing-machine can be built to execute the corresponding algorithm. Unfortunately it is impossible to build such a Turing-machine even in the simplest case.
Theorem: It is impossible to build a Turing-machine which could decide if an executable file in a RASPM with ABS contains a virus or not. (Leitold, 2000)
Proof: It is possible to create a RASPM or RASPM with ABS to simulate the Turing-machine. (Leitold, 2000) The modification of the expense functions of the procedures due to the simulation is irrelevant from the point of view of the proof of the theorem. Therefore let us create a program P in the RASPM with ABS which simulates the Turing-machine. This program writes a character 1 onto the output tape when the simulated Turing-machine stops in an acceptable state.
Let us make an easy virus, which is able to infect program files. Let the virus contain the mentioned program P in such way that at first P is executed as an answer for a random but fixed B input, then the virus starts running. It can be realised by attaching the virus to P, and inserting a JUMP command after each "write character 1" command of P. Thus the control is passed to the first command of the virus program. Let the virus program be so that it copies not only the virus program but also the program P and the fixed input B as well, in the event of infection.
According to this procedure, it is possible to create a program V in RASPM with ABS for any Turing-machine that becomes a virus if it can really be spread. It is obvious that program V can spread if program P and consequently the Turing-machine stops for the fixed input.
Let us suppose the opposite: there exists a Turing-machine T, which reads any program of RASPM with ABS and writes the character 1 out if the program contains a virus and writes the character 0 out if it does not. If the Turing-machine answers the input program V by the character 1 then program P or the corresponding Turing-machine will stop receiving the input B in any case. If the answer is 0, the corresponding Turing-machine will never stop. Therefore the Turing-machine is able to decide that an other Turing-machine will or will not stop as an answer for any input. However, this is impossible (Salomaa, 1985, Leitold, Csótai, 1992, Leitold, 2000)  .
.
The conclusion is the following: According to the Church theorem there is no way to build an algorithm for the detection of viruses. Now, we see that the virus detection problem defined above cannot be solved. Therefore, it is advisable to restrict the problem.
Let us assume that the size of infected files is limited. We are dealing only with viruses under this boundary and only these viruses should be detected. It means that the number of possible viruses is finite and even the number of possible virus samples is finite too. Theoretically the virus detection algorithm is able to store all possible virus samples so it can "easily" compare whether the suspicious file and one of its stored files is the same. If there is one of the stored files which is identical with the suspicious file then it means that the suspicious file includes a virus. On the other hand, if there is no stored file which is identical with the suspicious file then the suspicious file is virus free.
Note that this algorithm can not produce false positive or false negative. The only problem is the execution time of this algorithm. It is true that the number of stored virus samples used for the comparisons is finite but practically it is a very big number. The speed of this algorithm can be increased using the following modifications:
Using these modifications the algorithm is practically usable. The only problem is that the developer of the algorithm has to store all of virus body into the algorithm. This algorithm is widely distributed and of course the virus samples are distributed too. The developer is unable to protect the code and data of the algorithm safely, so the virus bodies can be restored. So only restricted information should be stored but it can yield false positive and negative.
The case of limiting the execution time of the virus is quite the same as limiting the space used by the virus. In this case the execution time is limited, so the virus can execute only a limited number of instructions. The only difference between the two reductions is that in this case the sequence of executed instructions should be stored completely with the data stored in the virus sample. This information should be stored in all cases, for all virus samples. This algorithm also does not produce false positive or false negative. Again, the only problem is the execution time of this algorithm - as was the main problem in the case of limiting the space used by the virus. The speed of this algorithm can be increased if only the instructions and data in the virus body are stored so there is no need to store the information about the host file. In the case of non-polymorphic viruses, only one item should be stored for each virus. And the number of items to store in the case of polymorphic viruses is decreased as well using this modification.
A possible simplification of the virus detection problem is if we deal with "several" known viruses only. In this case, the known viruses can also be used for the detection algorithm.
Let us take a series of code from each known virus, which emerges in every infected file when an infection takes place. Let be this series of code called a sequence. The task of the virus detection program is reduced to the search for these sequences in the program areas. Further problems emerge, however, concerning the algorithms of this principle:
It is obvious that the method can not be used for detection of polymorphic viruses and we have to look for other procedures for this purpose, but the method can be used for oligomorphic viruses. In this case the sequence for searching should be generated using the codes of the decoder function of the virus.
The quantity of false alarms depends on the length of the sequences and on the probability of finding specified values in specified cells of the program files. If the length of a sequence is N, the maximum n values can appear at equal probability, there are altogether M sequences, and the overall length of the examined files is L >> N, then the probability of finding any of the sequences in a file is:
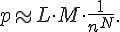
Let us examine now the expense criterion with which the sequence-searching algorithm
can be realised. Since computers often used in practice have fixed length of cells and
memory size (which is not the case for RASPM with ABS), the expense of each
command will be less than a constant value. It is recommended therefore to calculate
with uniform expenses. The sequence-searching algorithm compares the content of
each cell to be examined with the first cells of the sequences. If the examination is
executed separately, altogether
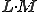 comparisons have to be performed. However, the sequences can be ordered according to the content of their first cells. Let us start the examination with the character in the middle position, and then follow the procedure into the right direction. Using this method in average only
comparisons have to be performed. However, the sequences can be ordered according to the content of their first cells. Let us start the examination with the character in the middle position, and then follow the procedure into the right direction. Using this method in average only 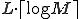 comparisons have to be carried out, provided the content of the first cells of sequences are different (
comparisons have to be carried out, provided the content of the first cells of sequences are different ( denotes the integer number not less then x). If identical values are found in the first cells of the sequences, the contents of the 2nd cells have to be examined as well. The expected value of the required further examinations is
denotes the integer number not less then x). If identical values are found in the first cells of the sequences, the contents of the 2nd cells have to be examined as well. The expected value of the required further examinations is 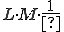 , therefore this is the number of the additional examinations required. If there is an identity found in the kth
examination, further
, therefore this is the number of the additional examinations required. If there is an identity found in the kth
examination, further 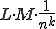 examinations are required. Therefore, the expected value of the altogether required examinations is:
examinations are required. Therefore, the expected value of the altogether required examinations is:
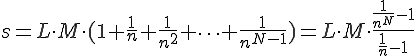
Considering the worst possible case, the maximum number of comparisons is 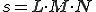 . Since the time requirement of the algorithm can be estimated by the number of comparisons, the sequence-searching algorithm can be realised in polynomial time.
. Since the time requirement of the algorithm can be estimated by the number of comparisons, the sequence-searching algorithm can be realised in polynomial time.
For identification of polymorphic viruses a simulation method can be used. The substance of the method is that the execution of the examined program file is started during the emulation (simulation) of the processor. A statistic is prepared about the executed commands, which is continuously compared to the existing statistics of known polymorphic viruses. When an agreement is found, a virus is detected. Based on this method, after encoding, the operation codes of the suspected program can be investigated. Compared to the sequence-searching process, no part of the series of codes is compared to known codes, but a statistic is prepared from the operation codes of a certain portion of the code is examined. In such a way the viruses can be identified even if parts of the commands are exchanged. However, in order to reach a safety of the search comparable to the sequence search method the statistics have to be based on much more operation codes.
However, the emulation type searching method can not be realised within polynomial time, since a virus can exist decoding routine of which is executed in exponential time, depending on a random number.
A possible method of searching unknown viruses is the processor emulating method mentioned for the polymorphic viruses. In this case, however, no statistics are prepared, but characteristic virus activity is watched. These typical characteristic virus activities are, e.g. when a program
The general virus detection problem is discussed in this paper. It is proven that the general virus detection problem can not be solved. It means that the virus detection problem should be simplified until it can be solved by an algorithm and therefore can be used in practice.
Two different possible reductions were highlighted at it was proved that they can be used for virus detection. Using the mentioned modifications of these algorithms, they are usable in the practice as well.
In the last part of this paper, two virus detection methods used in practice were provided. The sequence-searching algorithm can be solved in polynomial time, but this method can not be used for detection of polymorphic viruses. The other method is the simulation method, which can be used for detecting the polymorphic viruses as well, but this searching method can not be realised within polynomial times in all cases.