Fred Cohen
Computers & Security, 7(11) (1992), pp.641-652
ISSN 0167-4048
1992
 Download PDF (1.12Mb) (You need to be registered on forum)
Download PDF (1.12Mb) (You need to be registered on forum)* Funded by ASP, P.O. Box 81270. Pittsburgh, PA15217, USA.
In this paper, we propose a formal definition of "computer worms" and discuss some of their properties. We begin by reviewing the formal definition of "computer viruses", and their properties. We then define "computer worms" as a subclass of viruses, and show that many of the interesting ptoperties derived for viruses hold for worms. Finally, we summarize results, draw conclusions, and propose further work.
Keywords: Computer viruses, Computer worms.
An informal definition of "computer viruses" was first published in 1984 by Cohen [1], and was soon followed by his formal definition first published in 1985 [2] based on Turing's model of computation [3]. An alternative formal definition was proposed by Adleman [4] in 1989 based on set theory. In each of these cases, detection of viruses was shown to be undecidable, and several other results were derived.
These definitions were quite general in scope, and covered a broad range of replicating programs, possibly including the as yet only poorly defined, but widely used term "worm". Unfortunately, the lack of an adequate and standard definition of worms has created numerous misinterpretations and wasted time, and few of the results on worms have gone beyond the speculative phase. In this paper, we address this problem.
We begin here with an informal discussion by presenting a pseudo-code example of a very simple virus:
V:=[F=RANDOM-FILE-NAME; COPY V TO F;]
This virus simply replicates into files with random names, and is unlikely to be successful in any current computing environment because the chances are very poor that any of the replicas will ever be run. Even if they were run, they would not perform the functions the programs they replaced performed prior to replication, and thus would be rapidly detected. Since these replicas are of no practical value, they would likely be destroyed. More purposeful viruses, both malicious and benevolent, have been shown to be quite powerful, primarily due to their prodigious reliability and ability to spread. Viruses have also caused quite a problem in some environments.
The first published scientific references to computer worms that we are aware of came from Shoch and Hupp [5], who described several experiments with programs which replicated segments of themselves or parallel processing over a network. Unfortunately, no formal definition followed, and no sample code was provided. This left an unfilled void, and a host of informal but widely varying discussions using the poorly defined term followed in the literature.
Recently, the term "worm" has been widely used to describe programs that automatically replicate and initialize interpretation of their replicas.1 By contrast, the definition of viruses covers all self-replicating programs but does not address the manner in which replicas may be actuated. Here is a pseudo-code example of a simple worm:
W:=[F=RANDOM-FILE-NAME;COPY W TO F;RUN F;]
With the ability to replicate comes a host of other issues. The most obvious issue is that a replicating program might exhaust all of the available resources in a system, thus causing a system failure. In the case of this worm in a uniprocessing environment, the system eternally runs replicas of the worm, and no other processing can take place while the worm runs. In a multiprocessing environment, well-designed worms may be able to coexist safely with other programs if they are limited in their replication and evolution so as not to seriously impact performance.
Another important aspect of viruses is their ability to "carry" additional code with them. For example, in the 1984 paper [1], pseudo-code was provided for a compression virus, a denial of services virus, and other examples. The early worm experiments [5] solved large problems by including subprobems in replicas, thus allowing them to solve parts of the problem using remote resources. More commonly used viruses include the "diskcopy" program provided with the DOS operating system, which, in certain environments, replicates and carries along the contents of the entire disk on which it resides; product installation programs, which replicate as part of their installation process; and backup programs which make copies of themselves and other programs on other media to improve system reliability.
Another interesting feature of self-replicating programs is their resilience. In environments where non-replicating programs often fail or are destroyed through errors or omissions, viruses seem to thrive. This is because of the natural redundancy provided by replication. In this environment, viruses seem to be more fit than non-viral programs.
From a protection standpoint, viruses offer unique problems. Their resilience makes then very hard to remove from an operating environment, while their transitive spread bypasses most modern protection methods. General-purpose detection is undecidable [1,2,4], while special-purpose methods are not cost effective [9]. There are many other interesting properties of self-replicating programs. We refer the interested reader to some of the recent literature in this area [6].
In the remainder of this paper, we will formalize the notion of worms, describe how that formalism leads very quickly to a series of conclusions about worm properties, show how these results impact multiprocessing and multiprocessor environments, discuss some of the potentials for both malicious and benevolent worms, describe a number of historical incidents, summarize results, draw conclusions, and propose further work.
Cohen [2] presents "Viral Sets" in terms of a set of "histories" with respect to a given machine. A viral set is a set of symbol sequences which, when interpreted, causes one or more elements of the viral set to be written elsewhere on the machine in all of the histories following the interpretation. We include here some o the relevant definitions
required for the remainder of the paper, starting with the definition of a set of Turing-like [3] computing machines "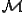 " as in Box 1.
" as in Box 1.
![\fbox{
\forall M [M \in \calM] \Leftrightarrow\\
\ \ M:(S_M,I_M,O_M:S_M\times I_M\mapsto I_M,N_M:S_M\times I_M\mapsto S_M,D_M:S_M\times I_M\mapsto d)\\
\ \ \ \ \begin{array}{ll}
\hspace{250}\\
\calN=\{0\dots\infty\} & \text{(the \quot{natural}\quot\ numbers)}\\
\calJ=\{1\dots\infty\} & \text{(the positive \quot{integers}\quot)}\\
S_M=\{s_0,\dots,s_n\},n\in\calJ & \text{(\calM\ states)}\\
I_M=\{i_0,\dots,i_j\},j\in\calJ & \text{(\calM\ tape symbols)}
\end{array}\\
\text{where}\\
\ \ \ \ \begin{array}{ll}
\hspace{250}\\
d=\{-1,0,+1\} & \text{\calM\ head motions)}\\
\not{S}:\calN\mapsto S_M & \text{(\calM\ state over time)}\\
\boxempty_M:\calN\times\calN\mapsto I_M & \text{(\calM\ tape contents over time)}\\
P_M:\calN\mapsto\calN & \text{(current \calM\ cell at each time)}
\end{array}\\
{\text{Box 1}}
}\\
\fbox{
\forall M\forall V (M,V)\in\calV\Leftrightarrow\\
\ \ \ \ [V\subset I^*] and [M \in \calM] and \forall v\in V \forall H \forall t,j \in \calN\\
\ \ \ \ [P_t=j] and [S_t=S_0] and (\boxempty_{t,j},\dots,\boxempty_{i,j+|v|-1}) = v \Rightarrow\\
\ \ \exists v'\in V, \exists t',t'',j'\in\calN\ and\ t'>t\\
\ \ \ \ (1)\ [[(j'+|v'|\le j] or [(j+|v|)\le j']] and\\
\ \ \ \ (2)\ [(\boxempty_{t',j'},\dots,\boxempty_{t',j'+|v'|-1}) = v'\ and\\
\ \ \ \ (3)\ [\exists t''[t\lt t''\lt t'] and [P_{t''}\in j',\dots,j'+|v'|-1]]\\
\text{Box 2}
}](../img/cache/d71cbcf676285c4439ca51c095a7204f.gif)
The "history" of the machine 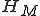 is given by
is given by 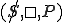 2 the "initial state" is described by
2 the "initial state" is described by 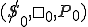 , and the set of possible
, and the set of possible 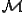 tape subsequences is designated by
tape subsequences is designated by 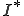 . We say that;
. We say that; 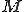 is halted at time
is halted at time 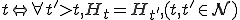 ; that
; that 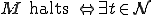 ,
, 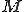 is halted at time
is halted at time 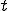 ; that
; that 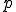 "runs" at time
"runs" at time 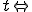 the "initial state" occurs when
the "initial state" occurs when 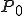 , is such that
, is such that 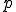 appears at
appears at 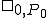 ; and that
; and that 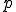 runs
runs 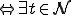 ,
, 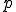 runs at time
runs at time 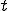 . The formal definition of the viral set (
. The formal definition of the viral set (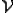 ) is given in Box 2.
) is given in Box 2.
The interested reader is referred to [2] for details.
We define a "Worm Set" 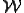 as a viral set in which any worm (
as a viral set in which any worm (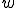 ) that is run at some move
) that is run at some move  results in a worm
results in a worm 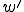 being run at some subsequent time
being run at some subsequent time 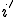 (Box 3).
(Box 3).
![\fbox{
\forall M \forall W (M,W) \in\calW \Leftrightarrow\\
\ \ \ \ [W\subset I^*] and [M \in \calM] and \forall w \in W \forall H \forall t,j \in \calN\\
\ \ \ \ [[P_t = j] and [S_t = S_0] and (\boxempty_{t,j},\dots,\boxempty_{t,j+|w|-1})=w] \Rightarrow\\
\ \ \exists w' \in W \exists t',t'',t''',j' \in \calN, t'>t\\
\ \ \ \ (1)\ [[(j'+|w'|\le j] or [(j+|w|)\le j']] and\\
\ \ \ \ (2)\ [(\boxempty_{t',j'},\dots,\boxempty_{t',j'+|w'|-1})=w'] and\\
\ \ \ \ (3)\ \exists t''[t\lt t'' \lt t'] and [P_{t''}\in j',\dots,j'+|w'|-1] and\\
\ \ \ \ (4)\ \exists t'''[t' \lt t'''] and [P_{t'''}=j'] and [S_{t'''} = S_0]\\
\text{Box 3}
}](../img/cache/830e77c7ea26fb7aa8a8784c7005a71c.gif)
Translated into English, this means (approximately):
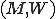 is a "worm set" if and only if:
is a "worm set" if and only if:
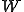 are
are 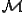 sequences -and-
sequences -and- 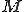 is a
is a 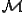 -and-
-and-
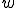 in
in 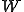 , for all histories of
, for all histories of 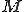 ,
,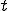 and cells
and cells 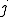
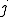 at time
at time 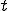 -and-
-and-
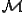 is in its initial state at time
is in its initial state at time 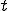 -and-
-and-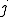 hold the worm
hold the worm 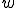 -then-
-then-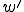 in
in 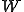 , a time
, a time 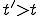 , and place
, and place 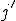 such that
such that
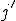 not overlapping worm
not overlapping worm 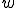
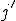 hold worm
hold worm 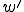 -and-
-and-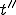 between
between 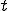 and
and 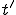 , worm
, worm 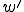 is written by
is written by 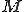 -and-
-and-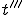 , worm
, worm 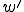 is run by
is run by 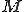
The definition of 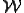 is different from that of
is different from that of 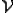 only in condition 4 being added, and because this term is an "and" on the right side of an implication,
only in condition 4 being added, and because this term is an "and" on the right side of an implication, 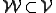 . We normally refer to elements of
. We normally refer to elements of 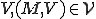 for a given machine M as "viruses" on M, and in the same parlance we will refer to members of
for a given machine M as "viruses" on M, and in the same parlance we will refer to members of 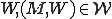 for a given machine M as "worms" on M. We typically drop the "on M" when we are referring to a particular M, and make statements like "all worms are viruses".
for a given machine M as "worms" on M. We typically drop the "on M" when we are referring to a particular M, and make statements like "all worms are viruses".
It turns out that most of the examples used for proofs about viruses [2] were not only viruses but also worms by the present definition, and thus the proofs apply directly. The remaining proofs do not depend on the lack of condition 4 above, and thus most of them arc also true for worms. For the purpose of brevity, we list some of the useful results for viruses that also hold for worms, along with page numbers from the cited work:3
 s is
s is  .
.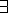 "largest"
"largest" 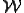 for any machine M.
for any machine M.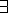 "smallest"
"smallest" 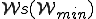 for some M.
for some M.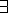
 of every size
of every size 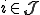 for a universal
for a universal  .
.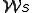 for some M.
for some M. computation.
computation.Another interesting result of this definition is that once a worm runs, M can never halt! More formally:4
Theorem A:
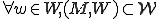 , w runs
, w runs 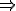 M never halts.
M never halts.
This is because at all times after w runs, there is always another 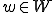 that must run at a subsequent time. More formally, assume
that must run at a subsequent time. More formally, assume 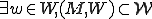 and w is run at time t. Then by condition 4 in the definition:
and w is run at time t. Then by condition 4 in the definition:
![\exists t'''>t:[P_{t'''}=j'] and [S_{t'''} = S_0]](../img/cache/569f286709929e865f6109407a758d0b.gif)
and by condition 2 of the definition:
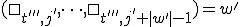
Thus 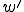 is run at time
is run at time 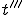 ! But if any
! But if any 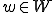 is run at any time t (specifically,
is run at any time t (specifically, 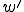 at time
at time 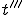 ), we return to the previous situation. By the induction theorem, if a condition is true at some time 1 and if being true at time t implies it is true at time t + 1, it is true for all time
), we return to the previous situation. By the induction theorem, if a condition is true at some time 1 and if being true at time t implies it is true at time t + 1, it is true for all time 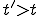 . By condition 3 of the definition:
. By condition 3 of the definition:
![\forall t \in \calN, \exists t'''>t : [S_{t'''}=S_0]\text{ and }\exists t''>t : P_{t''} != P_t](../img/cache/1890b151b700460129fdee0927b74d82.gif)
so by definition, 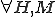 is not halted at time t, or in other words, M never halts. Thus a system running a worm has the "liveliness" property.
is not halted at time t, or in other words, M never halts. Thus a system running a worm has the "liveliness" property.
Lemma A.1:
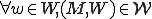 , M halts
, M halts 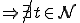 , w runs at time t.
, w runs at time t.
In a multiprocessing environment, worms are quite different than in a uniprocessing environment. For example, in a multiprocessing environment, a worm need not dominate processing. With proper controls on replication, a stable system can be put in place to attain desirable levels of worm activity. Here is a simple example in which a system function 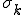 returns the number of currently active
returns the number of currently active 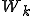 worms:
worms:
:= [WHILE TRUE DO [F=RANDOM-FILE-NAME;WHILE[
]WAIT]; COPY
TO F;RUN F;IF[
]EXIT;]]
In this case k limits the number of worms in the system. Each worm will replicate until k total worms are in the system. From that point on, each worm will wait until there are k or fewer worms in the system, replicate, and then exit. Assuming we have a fair scheduler and an accurate 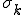 we get a relatively stable population of worms.
we get a relatively stable population of worms.
The 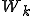 , worms could implement
, worms could implement 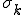 by updating a commonly accessible integer, by using unique process names in the process table, by associating themselves with files stored in a particular area, or by any other interprocess communication method available on the system.
by updating a commonly accessible integer, by using unique process names in the process table, by associating themselves with files stored in a particular area, or by any other interprocess communication method available on the system.
In order to model this sort of environment and show properties of worms, we require additional structure, but we don't want to abandon the mathematics associated with Turing machines in the process. This model extension is provided by the "Universal Protection Machine" [2] (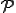 ), which is implemented on a universal
), which is implemented on a universal 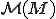 , and processes moves from each of a finite set of
, and processes moves from each of a finite set of 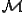 s simulated on M by using a "scheduler" and a "special state" which implements "system calls". This machine is defined as:
s simulated on M by using a "scheduler" and a "special state" which implements "system calls". This machine is defined as:
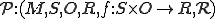
where:
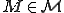 an "interpretation unit"
an "interpretation unit"
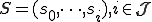 a set of "subjects"
a set of "subjects"
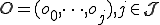 a set of "objects"
a set of "objects"
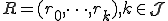 a set of "rights" of
a set of "rights" of 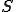 s over
s over 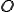 s
s
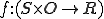 a protection matrix [8]
a protection matrix [8]
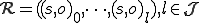 a "run sequence" of subjects "running" objects
a "run sequence" of subjects "running" objects
When a subject interprets an object (i.e., 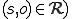 , M uses the rights of s for the duration of the interpretation of o. We are particularly interested in the rights "read" (r) and "write" (w), because these translate into the flow (f) of information between subjects. (i.e.,
, M uses the rights of s for the duration of the interpretation of o. We are particularly interested in the rights "read" (r) and "write" (w), because these translate into the flow (f) of information between subjects. (i.e., 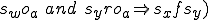 [10]. This is alternatively expressed as:
[10]. This is alternatively expressed as:
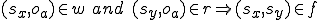
Information flow is transitive (i.e., 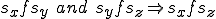 ) when M is a universal
) when M is a universal 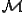 [2], and using this model a vital result that viruses can spread to the transitive closure of information flow from the source subject was derived.5 This is because
[2], and using this model a vital result that viruses can spread to the transitive closure of information flow from the source subject was derived.5 This is because 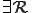 in which each subject in the transitive closure of information flow, in turn, interprets an object modified by the virus interpreted by a subject previously in the information flow from the original virus source.
in which each subject in the transitive closure of information flow, in turn, interprets an object modified by the virus interpreted by a subject previously in the information flow from the original virus source.
In any "fair" scheduler with unbounded work to be done and assuming that all accessible programs are run with some non-zero frequency, such an 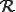 will eventually be realized because there will always be a partial subsequence of
will eventually be realized because there will always be a partial subsequence of 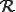 in which each of the necessary objects will be interpreted in sequence [2].
in which each of the necessary objects will be interpreted in sequence [2].
It turns out that the same result is, in general, true for worms, but transitivity doesn't result simply from running replicas. That is, if no object is modified by subjects running the worm, and if we ignore all other causal factors (e.g., a progenitor of a worm is run by some other user independent of the actions of the worm under consideration), only subjects with direct access to the worm can run it. Mathematically:
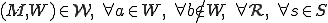
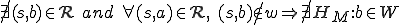
We will call worms that do not output to any objects "pure worms" (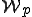 ).By definition,
s runs
).By definition,
s runs 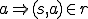 ,
,
so
Theorem B:
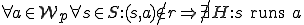
This implicitly assumes that R is static with respect to s and a over the period of the operation of the worm. If this is not the case, the situation may be far more complex because, in general, it is undecidable whether at some future time, 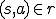 will be true [8]. This does not seem to be important in the short term; however, over the long term, there are often cases where momentary lapses in protection parameters could cause the undesired extension of rights. Once extended, of course, such rights cannot necessarily be revoked from a pure worm because the worm is operating with the authority of the subject that invoked it. Even though the right to invoke the worm may have been removed, all of the operating instances of replicas of the worm cannot necessarily be terminated without massive denial of service. This situation is partially covered by the "time transitivity" analysis used for viruses [10].
will be true [8]. This does not seem to be important in the short term; however, over the long term, there are often cases where momentary lapses in protection parameters could cause the undesired extension of rights. Once extended, of course, such rights cannot necessarily be revoked from a pure worm because the worm is operating with the authority of the subject that invoked it. Even though the right to invoke the worm may have been removed, all of the operating instances of replicas of the worm cannot necessarily be terminated without massive denial of service. This situation is partially covered by the "time transitivity" analysis used for viruses [10].
We anthropomorphize objects containing worms by sayin that a worm (w) has been granted the rights of a subject 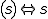 runs
runs 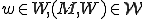 , and we express this as
, and we express this as 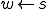 (read w gets s). If only the creator of a pure worm has direct access to it, it follows that the rights of all replicas will be limited to the rights of the originator, since only the originator can run it and, by definition, rights are only extended to objects by virtue of the subjects that interpret them. More generally, a pure worm only gets the subjects who run it:
(read w gets s). If only the creator of a pure worm has direct access to it, it follows that the rights of all replicas will be limited to the rights of the originator, since only the originator can run it and, by definition, rights are only extended to objects by virtue of the subjects that interpret them. More generally, a pure worm only gets the subjects who run it:
Lemma B.1:
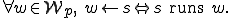
In the case of pure worms, evaluating the worst case impact of time variations on the protection state is trivial. Every subject that is ever granted direct access to w is potentially impacted, and all other subjects are completely safe from its direct impact. This model ignores performance impacts because the Turing machine model of computation generally assumes that moves take no time, and is used primarily to analyze the possibilities rather than the practicalities of any particular situation. A more realistic impact assessment is to assume that all users operating on all machines where there is an impacted user are impacted because of the performance degradation effects of the worm on those machines. This is an area for further research.
In a uniprocessing environment, because worms always run their replica, they are a bit harder to intentionally control than non-worm viruses because there is no obvious way to reduce the population. For viruses, however, this is not the case. For example, the following virus ( ) limits itself through the use of a name space:
) limits itself through the use of a name space:
:=[F=RANDOM-DIGIT;COPY
TO F;]
Since the digits consist only of (0...9), the total number of copies of 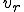 is limited (i.e., they overwrite each other). We can trivially extend this result to any finite-sized name space. Even a virus which optionally runs replicas can be controlled by a semaphore mechanism to adapt to the requirements of the environment. For example, the following viral variant (
is limited (i.e., they overwrite each other). We can trivially extend this result to any finite-sized name space. Even a virus which optionally runs replicas can be controlled by a semaphore mechanism to adapt to the requirements of the environment. For example, the following viral variant (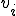 ) on the previous worm:
) on the previous worm:
:=[WHILE TRUE DO [F,F',F"=RANDOM-FILE-NAMES;IF[
]EXIT; IF[
][COPY
TO F AND F';RUN F AND F';];COPY
TO F";RUN F";]]
In this case, 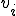 exists without replication while there are more than k replicas operating, and replicates at a higher rate if less than k/2 replicas are present. Thus, there is a stronger drive for replication when the population is low, while death becomes prominent when population is high. This too can be generalized to provide varying drives for survival of the species as a function of population.
exists without replication while there are more than k replicas operating, and replicates at a higher rate if less than k/2 replicas are present. Thus, there is a stronger drive for replication when the population is low, while death becomes prominent when population is high. This too can be generalized to provide varying drives for survival of the species as a function of population.
Most multiprocessing environments have mechanisms whereby one process can force another process to stop processing. These can be used by worms as a means of population control. For example, a pair of worms (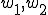 ) could be used to form a stable population ratio by spending some portion of their time forcing the other to halt (i.e., "kill" another process):
) could be used to form a stable population ratio by spending some portion of their time forcing the other to halt (i.e., "kill" another process):
:=[WHILE[
], KILL A
; PAUSE; REPLICATE;]
:=[WHILE[
], KILL A
; PAUSE; REPLICATE;]
As long as at least one of each 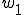 and
and 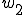 are active, and finding and killing processes takes far less than the duration of a "pause", the system will regain a balance at
are active, and finding and killing processes takes far less than the duration of a "pause", the system will regain a balance at 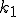 and
and 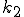 respectively of
respectively of 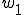 and
and 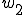 . If instead of simply waiting, each worm performed some useful functions requiring relatively little time, we would have a useful worm computation environment. We can call this a 2-worm system, and it is simple to extend the principle to an n-worm system as follows:
. If instead of simply waiting, each worm performed some useful functions requiring relatively little time, we would have a useful worm computation environment. We can call this a 2-worm system, and it is simple to extend the principle to an n-worm system as follows:
:=[
[WHILE [
], KILL A
;]; PAUSE; REPLICATE;]
By making an n-worm system for large n, we may dramatically improve overall system reliability. In one experimental implementation, we used an n-worm to perform regular maintenance tasks on a Unix™ system. In this case, the worms deleted old temporary files and "core" files, regenerated databases, killed errant processes, and performed other regular maintenance functions. The result was an "ecosystem" in which almost no systems administration was required for continued operation over a four-year period.
Despite the potential practicality of worms in multiprocessing environments, we have encountered more destructive worms than practical ones in the global multiprocessing environment, and early experiments with practical worms have occasionally resulted in problems. In 1985, an experimental worm in a Unix™ environment replicated until the maximum number of processes available to the user were consumed. At that point, all of the replicas were forced into a wait state because they could not create new replicas until some other replica failed. It turned out that in this case there was no way to stop the worm except through a system reboot, because we couldn't kill all of the processes simultaneously, and as soon as one was killed, another replica was created. The inherent priorities of the scheduler made the problem unresolvable. This worm did no serious harm, because all of the replicas were in wait states, and consumed no critical resource.
Another worm which impacts multiprocessing environments is commonly called a "paging monster". A paging monster simply copies itself into each of a series of pages in memory, cycling through memory periodically. In most paged virtual memory systems, this worm forces the system paging program to page out other processes at a very high rate, and thus forces the system to thrash. By combining the Unix™ worm described above with the paging monster, the situation can become far more damaging, because you cannot eliminate the paging monsters by simply killing processes.
We return for a moment to Lemma B.1. In each of the examples given above, the worms were pure worms run by a single user, and although they had an impact on the system, in each case, no rights were extended to them beyond those granted to the user who created them. By directly limiting the impact of a single user on system behavior and prudent use of standard access controls, we can protect users in a multiprocessing environment from severe damage due to pure worms. We don't have to worry about the transitive closure of rights in this case.
There is a temptation to try to extend Lemma B.1 to cover non-pure worms whose modifications to other objects don't cause those objects to include worms, but this doesn't work for two reasons. The
first reason is that any modification could be interpreted by some M' simulated by interpreting some third object so as to make the modification introduce a worm for machine M'. For any universal 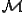 , there always exists such an M'. The second reason is that we would have to exclude all modifications that might eventually result in the generation of a worm. For example, multiple separate and independent modifications, none of which introduces a worm for some machine M, could generate a worm through their combined action. The only cases where we may be able to extend Lemma B.1 are cases where M is not a universal
, there always exists such an M'. The second reason is that we would have to exclude all modifications that might eventually result in the generation of a worm. For example, multiple separate and independent modifications, none of which introduces a worm for some machine M, could generate a worm through their combined action. The only cases where we may be able to extend Lemma B.1 are cases where M is not a universal 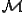 , which is of relatively little interest in most modern computing environments; and the case where information flow is closed under transitivity.
, which is of relatively little interest in most modern computing environments; and the case where information flow is closed under transitivity.
Just as multiprocessing environments provide unique opportunities for worms and viruses to perform useful or malicious functions, multiprocessor environments have features that impact the effectiveness of worms and viruses. There are several important cases in the modern environment to consider because of their large numbers. They are (loosely):
We don't yet know a great deal about protection from worms and viruses on these systems other than the general results previously published on viruses. There are, however, some interesting points to be made and some possible areas of research to be explored.
In tightly coupled systems, processors are essentially not distinguishable from a protection standpoint, and thus they can be treated as a single system. At the other extreme, in file transfer and forward systems, remote processors have limited functionality, and while they can be impacted by large numbers of network requests, livelock, and deadlock of the network, etc., with nominal protection in the form of setting low priorities for remote file transfers and limited function interfaces for incoming files, almost all impact from remote systems can be eliminated.
Systems allowing remote logins dominate in the timesharing arena, with almost every timesharing system now providing remote login over modems, and networked systems allowing remote login through explicit "remote shell" and "remote login" network calls. In much of the modern computing environment, remote login is permitted to known users without additional authentication, and in cases where this is not typical it is common to provide login scripts for accessing remote systems using known user identities and passwords. The increased standardization of this process makes the extension of rights from machine to machine very simple.
For example, it is simple to write a worm program that attempts remote logins to hosts which are allowed to login to the current host (since reciprocity is the norm in the modem computing environment). Assuming this has some success, the worm can replicate into the new system and operate from there, attempting to extend privileges to a new machine. By combining this mechanism with known attacks, the worm may attempt to attain increased privilege. Once increased privilege is attained, the worm has more candidates available for remote access and thus mechanism to extend privilege still further. A simple that guesses passwords on remote machines once access is attained works quite well because, typically, password protection is relatively minimal and a list of user identities and limited information on the users is commonly available. A lack of audit trails against this sort of attack also helps keep the attack simple and effective.
The mechanism of remote procedure calls is often used to implement multiprocessor operations in networks where special services exist in special machines. For example, a local mail server may store all of incoming mail and keep desired mailing lists available so that the information doesn't have to be duplicated throughout the network, and it is common to provide remote printer access so that expensive that don't have to be duplicated can be shared. The key here is that the remote operation is made very automatic and transparent so that user convenience is maximized. This in turn provides capabilities on remote processors for local processing power, file storage, and other system resources. To the extent that the implementation is less than ideal, this grants possibilities for worm and viral exploitation.
A shared file system provides a means by which a user can make a worm available to a multitude of users with great transparency. For example, by planting a worm in a program called "ls"6 and offering users access to another program in the same directory, many users may be fooled into changing to that directory and running "ls". When they do that, and assuming their search path7 is set up as most Unix users' search are set up, the local "ls" will be run, which will invoke the worm. If the designer a bit clever, the "ls" worm will first delete or rename itself, then perform the system's "ls" command, and then replace itself, thus keeping its presence hidden to the casual observer.
The effect of the shared file system is to make this sort of access far more likely and casual. In most shared file system environments, this mechanism can be used to effectively impact all of the machines in the environment. A shared file system, even if most of it is read-only to any given user, provides a very high bandwidth and easy-to-exploit environment for worms and viruses. It facilitates the execution of programs by remote processors under conditions that grant the program access to the remote user's privileges instantly and with no additional authentication required. Even a pure worm can spread throughout such a system with relative ease, and a virus that "infects" files should typically be able to take over the entire network of shared file system machines in very short order. Based on the timesharing experiments with viruses [1], it would not be surprising to see the vast majority of the network fall to attack in under an hour.
The current trend in distributed computing environments is toward the shared file system situation, and without some substantial effort to provide protection in this environment this is a disaster waiting to happen. The current protection techniques, which effectively allow a systems administrator to prevent read or write access to a file system or on a directory or file basis restrict access to particular areas of a file system, are completely inadequate for protection against viruses and worms. In the current environment, each site protects itself only against intrusion caused by outside agents, whereas in the case of worms and viruses the intrusion comes from inside agents (i.e., the users on the impacted system running external programs).
Remote process invocation makes the problem of malicious worm control in a multiprocessor environment far more difficult. As examples, the Unix™ remote procedure call facility, the Novelle NetWare™ add-on packages that allow remote command execution on workstations, and the DecNet™ remote command interface, each provide rich environments for uncontrolled worm spread.
Even though these systems may limit the authorized remote users who may invoke these facilities, this is ineffective against worms because they spread transitively. Thus, unless the transitive closure of machines with users authorized for remote process invocation is a closed subset of the systems or none of the users ever runs a worm, all of the members of the environment are susceptible. Here we see that in the case of worms in a remote process invocation environment, just as in the case of viruses in general, transitive spread results in a partially ordered set of infectable users from any given source, and just as in the case of viruses, nearly all of the networked computers in the world today are susceptible.
Even very simple worms in the environment today wreak widespread havoc, and just as viruses may evolve in a very general fashion thus making eradication very difficult, worms may evolve with the same generality. In the case of worms, the problem is particularly unnerving because of the requirement for concerted action throughout a distributed network.
For example, the Internet worm [6], which did not evolve, required concerted action, but this action was made easy because the attack depended on a "bug" which was easily repaired, and because all of the replicas were essentially identical. If this worm had evolved during replication in a substantial manner, and had not depended on a "bug", but rather on the legitimate rcmotc procedure call capability of Unix™, the eradication problem would have been far more severe. The worm experiments that went awry at Xerox [5] required a concerted network-wide reboot and the Unix™ worm described earlier required a system reboot.
Returning again to Lemma B.1, even in the casts of these relatively severe network worms no extension of privileges was achieved. In other words, the systems extended the privileges exploited by these worms to their originator, either by design or implementation error. The worms did not gain privileges by being run unknowingly by users with special rights, they were granted system rights by exploiting flaws in the systems they attacked.
We have provided a mathematical definition of "computer worms" that we feel reflects the current usage and reconciles many of the inconsistencies in recent literature. We have listed several important properties of worms and systems containing worms, and derived several new results that are specific to specific sorts of worms. We have shown several methods by which self-controlled worms and viruses can coexist with other programs in multiprocessin and multiprocessor environments, and that wea L esses exist in current multiprocessing environments which facilitate uncontrolled worm spread.
In future papers, we hope to present theoretically sound defenses for specific subclasses of worms and criteria for the safe coexistence of some viruses and non-viral programs. A number of other subclasses of viruses also appear to be of interest, and we believe that theoretical results may guide us toward improved defenses against many subclasses of viruses currently exploited by attackers.
We encourage other researchers to examine and challenge our definition with mathematical alternatives. As we stated earlier, the lack of a mathematical definition has caused numerous problems in this area, and we hope that this presentation of one will lead to substantial progress.
Fred Cohen received a B.S. in Electrical Engineering from Carnegie-Mellon University in 1977, an M.S. in Information Science from the University of Pittsburgh in 1981, and a Ph.D. in Electrical Engineering from the University of Southern California in 1986. He was a professor of Computer Science and Electrical Engineering at Lehigh University from January 1985 through April 1987, and a professor of Electrical and Computer Engineering at The University of Cincinnati from September of 1987 through Dccembcr of 1988. He is currently the President of ASP in Pittsburgh, PA, U.S.A.
Dr. Cohen has published over 20 refereed papers and over 20 other professional articles, has written several graduate level texts, and has designed and implemented numerous devices and systems for information protection. He is most well known for his ground-breaking work in compurcr viruses. where he did the first in-depth mathematical analysis, performed many startling experiments which have since been widely confirmed. and developed the first protection mechanisms, many of which are now in widespread use. His current rcscarch interests are concentrated in high integrity systems.
1 This idea was first brought to my attention in a paper published in Computers and Security in which Thomas A. Longstaff and E. Eugene Schultz describe several "worms".
2 "For convenience, we drop the M subscript when we are dealing with a single machine except at the first definition of each term.
3 Some of these require a trivial modification to the sample M so that instead of halting after replicarion, M moves the tape head to rhe start of the replica and changes to state 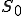 .
.
4 We use letters for theorems and lemmas herein to avoid conflicts with the theorem numbering from cited works.
5 Page 35 [2].
6 "ls" is the name of the Unix directory program used by most users to see what files are in a directory. "ls" is also the most frequently run program under Unix according to statistics taken in the first virus experiments in 1984.
7 The scqucncc of places the command interpreter looks to find a program.
[Back to index] [Comments (0)]